Teorema dell'equivalenza dei parallelogrammi
Due parallelogrammi sono equivalenti se hanno le basi e le altezze corrispondenti congruenti.
E' uno dei criteri di equivalenza più noti.
Un esempio pratico
Considero questi due parallelogrammi.
Pur avendo forme diverse, entrambi i parallelogrammi hanno la stessa base (b=5) e altezza (h=3) corrispondente.
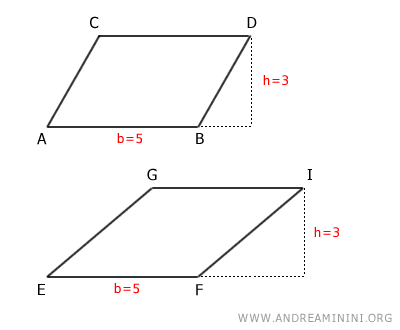
Quindi, la loro superficie è la stessa.
Per verificarlo basta osservare la formula dell'area del parallelogramma.
$$ A = b \cdot h $$
Dove "b" è il lato preso come base e "h" è l'altezza del parallelogramma.
$$ A = b \cdot h = 5 \cdot 3 = 15 $$
Il risultato è lo stesso per entrambi i parallelogrammi.
La dimostrazione
Per dimostrare questo teorema, considero due parallelogrammi ABCD ed EFGI.
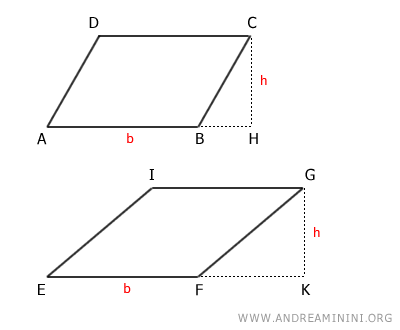
Per ipotesi iniziale, i due parallelogrammi hanno la base congruente e l'altezza congruente.
$$ \overline{AB} \cong \overline{EF} $$
$$ \overline{HC} \cong \overline{KG} $$
Devo dimostrare che i due parallelogrammi sono equivalenti, ovvero che hanno la stessa estensione di superficie (area).
Per farlo sovrappongo le basi AB ed EF dei due parallelogrammi con un movimento rigido.
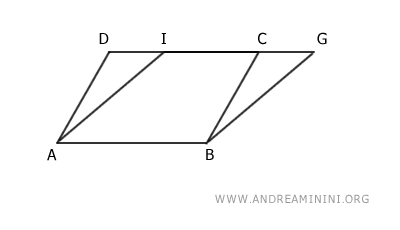
Dalla sovrapposizione emergono due triangoli ADI e BCG.
Gli angoli α e β dei triangoli sono congruenti, perché i lati degli angoli sono paralleli e concordi, in quanto coincidono con quelli dei parallelogrammi che per definizione sono tra loro paralleli AD≅BC e AI≅BG.
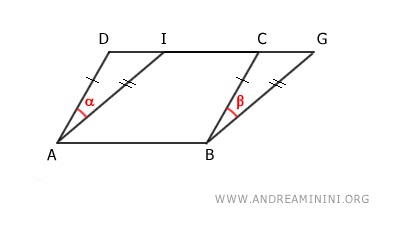
Quindi, per il primo principio di congruenza i due triangoli ADI≅BCG sono congruenti, perché hanno due lati AD≅BC e AI≅BG congruenti e l'angolo α≅β tra di essi congruenti.
$$ ADI \cong BCG $$
Ora, la superficie del parallelogramma ABCD posso vederla come la differenza tra il trapezio ABGD e il triangolo BCG
$$ ABCD \doteq ABGD - BCG $$
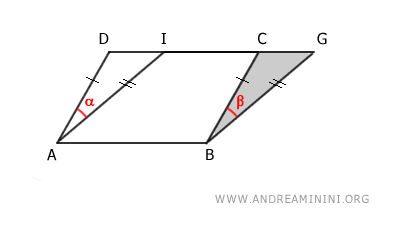
Allo stesso modo la superficie del parallelogramma ABGI posso considerarla come la differenza tra il trapezio ABGD e il triangolo ADI.
$$ ABGI \doteq ABGD - ADI $$
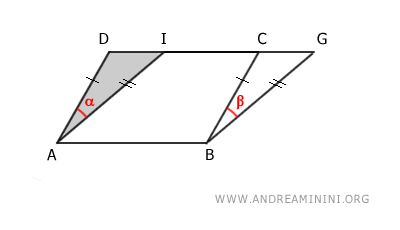
Sapendo che i triangoli ADI≅BCG sono congruenti, posso dedurre che la superficie dei parallelogrammi ABCD e ABGI è la stessa (superficie equivalente), perché sono entrambe ottenute tramite la differenza di due poligoni tra loro congruenti.
$$ ABCD \doteq ABGD - BCG \doteq ABGD - ADI \doteq ABGI $$
$$ ABCD \doteq ABGI $$
Sapendo che per costruzione i parallelogrammi ABGI≅EFGI sono congruenti, deduco che anche i due parallelogrammi iniziali ABCD e EFGI sono poligoni equivalenti, ovvero hanno la stessa estensione di superficie.
$$ ABCD \doteq EFGI $$
Osservazioni
Alcune osservazioni, corollari e note a margine
- Due rettangoli sono equivalenti se hanno le relative basi e altezze congruenti
I rettangoli sono due casi particolari di parallelogrammi che hanno gli angoli interni retti. Quindi, il teorema dell'equivalenza dei parallelogrammi è applicabile anche ai rettangoli.
E così via.
