Triangoli
Un triangolo è un poligono composto da tre lati e tre angoli.
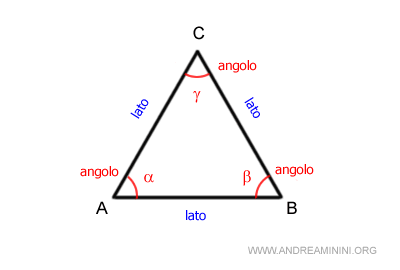
Le caratteristiche
Il triangolo è un insieme di punti delimitati da una poligonale chiusa ed è uno dei più semplici e fondamentali oggetti in geometria euclidea.
I punti estremi dei lati sono tre punti non allineati (A, B, C) detti vertici.
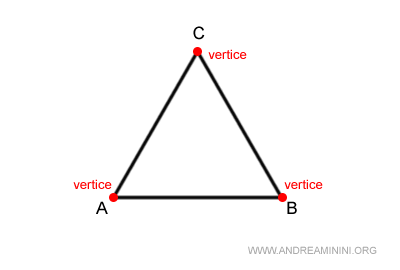
Un vertice è detto vertice opposto a un lato se non appartiene al lato stesso.
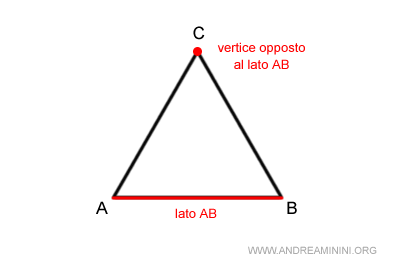
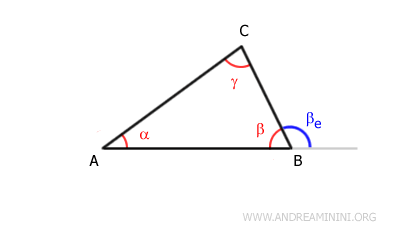
A ogni coppia di lati è associato un angolo interno che ha per vertice un vertice del triangolo e per lati i due lati del triangolo.
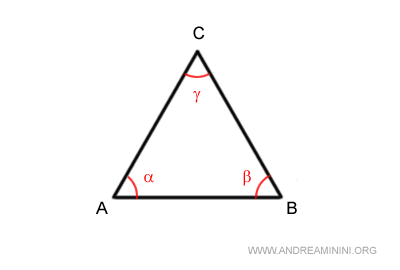
Un angolo è detto angolo adiacente a un lato se il vertice dell'angolo coincide con uno degli estremi del lato e uno dei lati dell'angolo coincide con il lato stesso.
Ad esempio, l'angolo β è adiacente sia al lato AB che al lato BC.
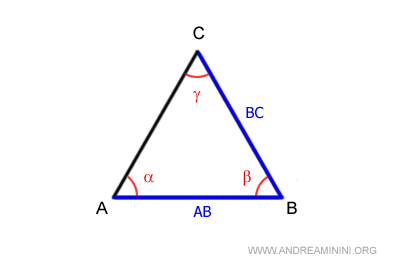
Pertanto, in ogni lato del triangolo ci sono due angoli adiacenti al lato.
Ad esempio, sono adiacenti al lato AB gli angoli α e β.
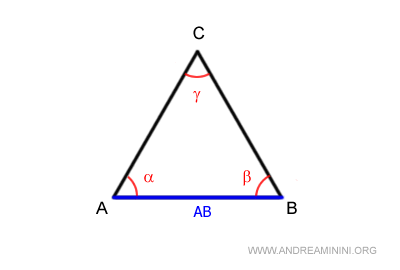
Un angolo è detto angolo opposto al lato se non è adiacente al lato.
Ad esempio, l'angolo γ è opposto al lato AB.

Indipendentemente dalla forma del triangolo, la somma degli angoli interni di un triangolo è sempre pari a 180°.
$$ \alpha + \beta + \gamma = 180° $$
A ogni angolo interno del triangolo è associato un angolo esterno corrispondente.
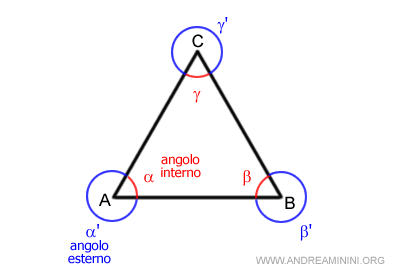
Il termine "triangolo" deriva dalle parole greche "tri", che significa "tre", e "angolo", che significa "angolo". I triangoli hanno una vasta gamma di usi e applicazioni in molteplici campi (es. fisica, matematica, ecc.). I triangoli sono anche fondamentali nello studio della trigonometria, un ramo della matematica che esamina le relazioni tra i lati e gli angoli dei triangoli.
Tipi di triangoli
I triangoli possono essere classificati in vari modi.
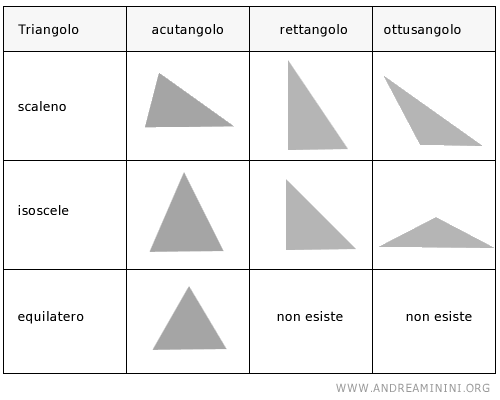
In base ai lati:
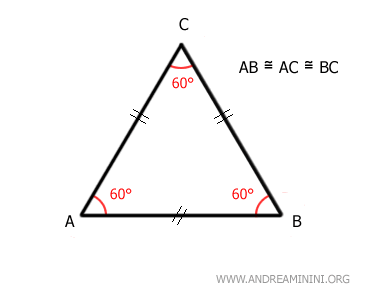
- Triangolo equilatero
E' un triangolo con tutti e tre i lati congruenti. In un triangolo equilatero, tutti e tre gli angoli sono di 60 gradi.
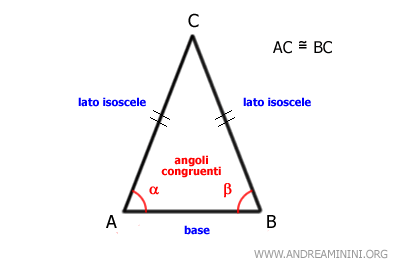
- Triangolo isoscele
E' un triangolo con due lati congruenti. Un triangolo isoscele ha anche due angoli congruenti adiacenti alla base.
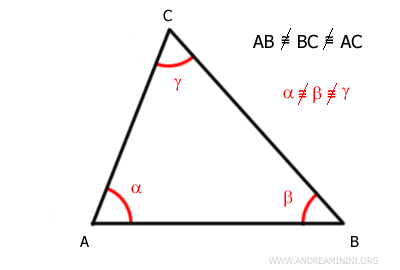
- Triangolo scaleno
E' un triangolo con tutti e tre i lati di lunghezze diverse ossia non congruenti.
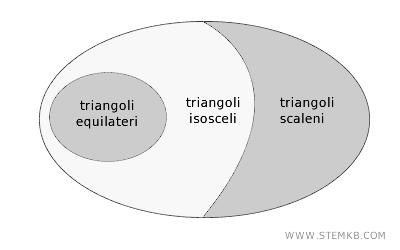
Nota. Il triangolo equilatero, che presenta tre lati uguali, rappresenta un caso particolare di triangolo isoscele. Di conseguenza, l'insieme dei triangoli equilateri è contenuto in quello dei triangoli isosceli, il che implica che la classificazione dei triangoli in base ai lati non costituisce una partizione.
In base agli angoli:
- Triangolo acutangolo
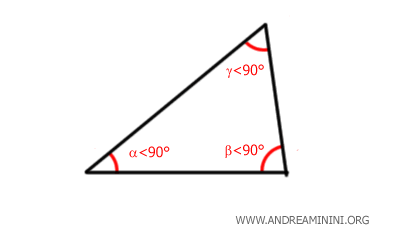
E' un triangolo in cui tutti gli angoli sono acuti (meno di 90 gradi).
- Triangolo ottusangolo
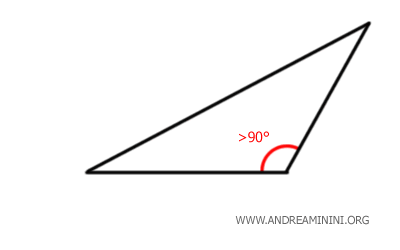
E' un triangolo con un angolo ottuso (più di 90 gradi).
- Triangolo rettangolo
E' un triangolo con un angolo retto (90 gradi).
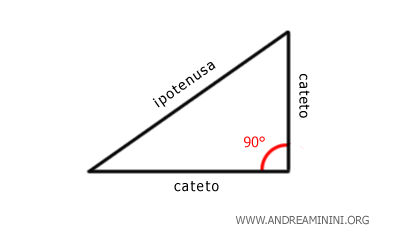
Solo nel caso del triangolo rettangolo i lati che formano l'angolo retto (90°) sono detti "cateti", mentre il lato opposto all'angolo retto è detto "ipotenusa".
Le formule
In generale le formule per calcolare le grandezze di un triangolo
- Area
L'area (A) di un triangolo si calcola utilizzando la formula: base (b) per altezza (h) diviso due $$ A = \frac{\text{b} \cdot \text{h}}{2} $$In alternativa, se conosco solo le lunghezze dei lati posso utilizzare la formula di Erone. $$ A = \sqrt{p(p-l_1)(p-l_2)(p-l_2)} $$ Dove \( l_1 \), \( l_2 \), e \( l_3 \) sono i lati e \(p = \frac{l_1+l_2+l_3}{2}\) è il semiperimetro del triangolo.
- Perimetro
Il perimetro (P) di un triangolo è la somma delle lunghezze dei suoi lati. $$ P = a+b+c $$ Dove a,b,c sono le lunghezze dei tre lati del triangolo.
Nel caso del triangolo isoscele ed equilatero si possono usare formule particolari per calcolare l'area e il perimetro.
I centri o punti notevoli del triangolo
Il triangolo ha vari centri significativi, detti punti notevoli, come il baricentro, il circocentro e l'incentro.
- Ortocentro
Le tre altezze di un triangolo si incontrano in un punto detto ortocentro.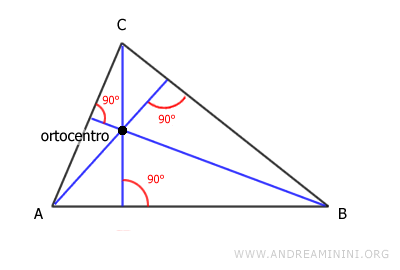
Nota. Ogni triangolo ha tre altezze. L'ortocentro può trovarsi all'interno o all'esterno del triangolo, oppure su un vertice. E' un punto esterno al triangolo nel triangolo scaleno ottusangolo. E' un punto interno nel triangolo scaleno acutangolo. Coincide con il vertice dell'angolo retto nel triangolo scaleno rettangolo.
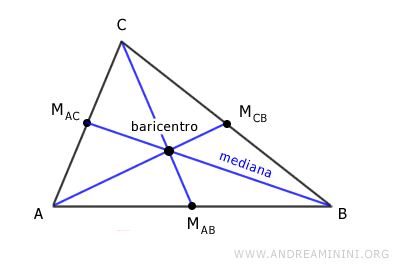
- Baricentro
In un triangolo le tre mediane si incontrano in un punto interno del triangolo detto baricentro.
- Incentro
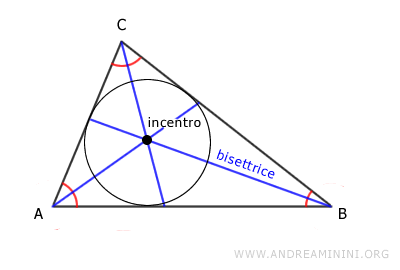
Le tre bisettrici di un triangolo si intersecano in un punto di incontro detto incentro. L'incentro coincide con il centro della circonferenza inscritta al triangolo.
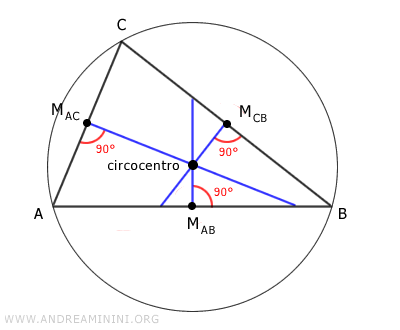
- Circocentro
In un triangolo i tre assi si intersecano in un punto interno al triangolo detto circocentro. Il circocentro è il centro della circonferenza circoscritta al triangolo.
Questi quattro punti (ortocentro, baricentro, circocentro e incentro) sono conciclici, cioè giacciono sulla stessa circonferenza, chiamata circonferenza di Euler.
Come ricordarsi i punti notevoli del triangolo? Per memorizzarli, ho ideato una frase in cui l'iniziale di ogni parola corrisponde a un punto notevole, mentre la lettera iniziale della parola successiva suggerisce il metodo per trovarlo:
"BAsta MEttere ORdine ALmeno IN BIblioteca Con AStuzia"
- BA = Baricentro → si trova con le ME = mediane.
- OR = Ortocentro → si trova con le AL = altezze.
- IN = Incentro → si trova con le BI = bisettrici.
- C = Circocentro → si trova con gli AS = assi.
Questa associazione aiuta a ricordare facilmente i punti notevoli e il loro metodo di costruzione.
Le proprietà dei triangoli
Alcune osservazioni e proprietà importanti dei triangoli in geometria.
- La somma degli angoli interni di un triangolo è sempre uguale a 180° gradi
In altre parole, la somma degli angoli interni di un triangolo è sempre uguale a un angolo piatto. Questa proprietà vale per qualsiasi tipo di triangolo. $$ \alpha + \beta + \gamma = 180° $$
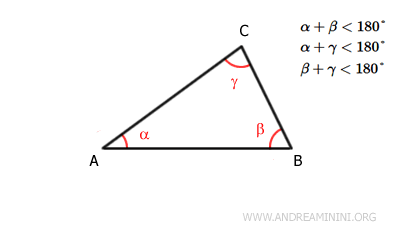
- La somma di due angoli interni è inferiore a 180°
In un triangolo la somma di due angoli interni qualsiasi è sempre inferiore di un angolo piatto (180°).
- Un triangolo ha sempre almeno due angoli acuti
Un triangolo ha sempre almeno due angoli acuti perché non può avere più di un angolo retto o di un angolo ottuso. In caso contrario, la somma di due angoli sarebbe maggiore o uguale a 180° (angolo piatto), violando il teorema della somma di due angoli interni inferiore a 180°.Dimostrazione. Gli angoli alla base di un triangolo sono sempre acuti per una semplice ragione legata alla somma degli angoli interni del triangolo, che è sempre 180°. Se un triangolo ha un angolo retto (90°), allora gli altri due angoli devono sommarsi a 90° (perché \(180° - 90° = 90°\)). Questo significa che entrambi devono essere minori di 90°, quindi acuti. D'altra parte, se un triangolo ha un angolo ottuso (maggiore di 90°), allora la somma degli altri due angoli deve essere inferiore a 90° perché \(180° \) meno un angolo ottuso è minore di 90°. Quindi, ciascuno di questi angoli sarà minore di 90°, cioè acuto. In conclusione, gli angoli alla base di un triangolo non possono mai essere retti o ottusi perché ciò violerebbe la regola della somma degli angoli interni. Di conseguenza, sono sempre acuti.
- Teorema dell'angolo esterno
In un triangolo ogni angolo esterno (βe) è maggiore di ciascuno degli angoli interni non adiacenti (α e γ).
- Teorema di Pitagora
In un triangolo rettangolo, il quadrato della lunghezza dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati delle lunghezze degli altri due lati. - Il triangolo è sempre inscrivibile in una circonferenza
Se disegno un triangolo ABC e traccio le bisettrici degli angoli, queste si incontrano sempre in un unico punto, detto "incentro", equidistante dai lati. Pertanto, l'incentro è il centro di una circonferenza inscritta nel triangolo.

- Il triangolo è sempre circoscrivibile a una circonferenza
Se disegno un triangolo ABC e traccio gli assi sui lati, ovvero le perpendicolari ai lati passanti per i loro punti medi, questi si incontrano sempre in un unico punto, detto "circocentro", equidistante dai vertici. Pertanto, il circocentro è il centro di una circonferenza circoscritta intorno al triangolo.

Nota. Nel caso particolare di un triangolo equilatero esiste una relazione tra il raggio della circonferenza inscritta (r) e il raggio della circonferenza circoscritta (R) $$ r = \frac{1}{3} \cdot R $$ Questa formula è valida perché in un triangolo equilatero il rapporto tra i raggi delle due circonferenze è costante. Il baricentro, l'ortocentro, il circocentro e l'incentro coincidono in un unico punto (O).
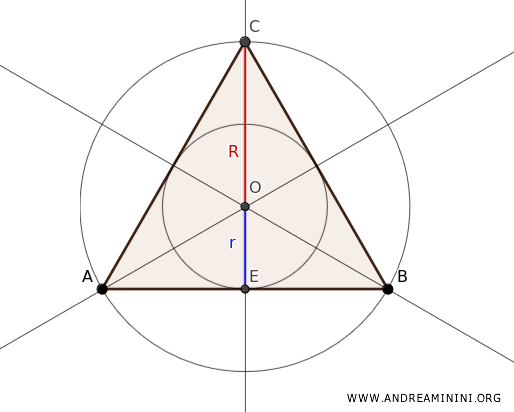
Quindi, il circocentro e l'incentro si trovano entrambi al centro del triangolo, ma i raggi delle due circonferenze sono diversi. Sapendo che il baricentro divide ogni mediana (es. EC) in due parti, una doppia dell'altra, deduco che $ R = 2r $. In questo caso posso scrivere l'altezza del triangolo ABC come $ h = r+R $ e poiché $ R=2r $ ottengo che $ r=1/3⋅R $. - Ogni triangolo ha un unico centro di gravità, o centroide, che si trova all'incrocio delle sue mediane (le linee tracciate dal vertice al punto medio del lato opposto).
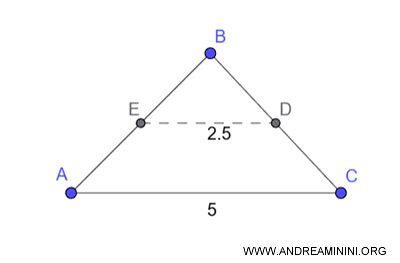
- Il segmento tra due punti medi del triangolo è parallelo e congruente alla metà del terzo lato
Il segmento $ ED $ che unisce i punti medi di due lati ( $ AB $ e $ BC $ ) di un triangolo è parallelo ed è lungo la metà del terzo lato $ AC $.
- Teorema del triangolo isoscele
Se un triangolo ha due lati congruenti, allora anche gli angoli opposti a questi lati sono congruenti.Esempio. Un triangolo isoscele è caratterizzato dalla congruenza dei suoi lati obliqui e dei corrispondenti angoli alla base. Poiché ciascun angolo alla base è opposto a uno dei lati obliqui, ne consegue che in un triangolo gli angoli opposti a due lati congruenti sono sempre uguali tra loro.

Nel triangolo isoscele gli angoli alla base sono congruenti perché derivano dalla simmetria del triangolo rispetto alla sua altezza, che funge da asse di simmetria.
E così via.
