La partizione di un insieme

partizione P(A)

nessun sottoinsieme è un insieme vuoto
l'unione dei sottoinsiemi è uguale all'inseme A
i sottoinsiemi sono insiemi disgiunti tra loro, ossia non hanno elementi in comune

La partizione di un insieme in due sottoinsiemi è detta bipartizione.

La partizione in tre sottoinsiemi è detta tripartizione.

Una generica partizione in k sottoinsiemi è detta k-partizione.

Nota. Non esiste un'unica partizione dell'insieme. Un insieme di k elementi può essere suddivido in k! fattoriale partizioni.

Un esempio pratico
Il calcolo del numero delle partizioni
Osservazioni

Un esempio pratico

Considero l'insieme finito A composto da 5 elementi

$$ A = \{ 1,2,3,4,5 \} $$

Una partizione dell'insieme è la seguente bipartizione

$$ P(A) = \{ \ \{ 1,2,3 \} \ , \ \{ 4,5 \} \ \} $$

Utilizzando i diagrammi di Eulero-Venn la bipartizione si rappresenta in questo modo:

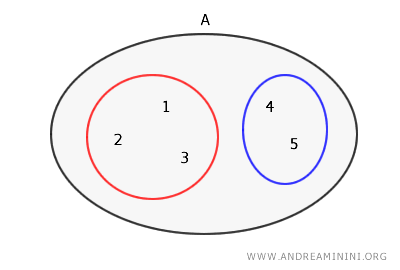
un esempio di bipartizione

Verifica. La partizione è composta da due sottoinsiemi {1,2,3} e {4,5} non vuoti. I due sottoinsiemi sono disgiunti $$ \{ 1,2,3 \} \cap \{4,5 \} = Ø $$ L'unione dei sottoinsiemi della partizione è uguale all'insieme A $$ \{ 1,2,3 \} \cup \{4,5 \} = \{ 1,2,3,4,5 \} = A $$

L'insieme è composto da 5 elementi. Quindi, esistono 52 partizioni possibili secondo il numero di Bell B₅.

Ad esempio, un'altra partizione è la seguente. Anch'essa è una bipartizione.

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4,5 \} \ \} $$

Un'altra partizione è la seguente tripartizione

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4 \} \ , \ \{ 5 \} \ \} $$

Questa è invece una 4-partizione perché l'insieme è suddiviso in 4 sottoinsiemi

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3 \} \ , \ \{ 4 \} \ , \ \{ 5 \} \ \} $$

Complessivamente ci sono 52 combinazioni possibili degli elementi (partizioni) dell'insieme A.

Il calcolo del numero delle partizioni

Il numero di partizioni di un insieme finito $ A $ con $ n $ elementi è dato dal numero di Bell $ B_n $, che può essere calcolato usando la seguente formula ricorsiva con $ B_0 = 1 $ come condizione iniziale.

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

In questa formula:

$ \binom{n-1}{k} $ è un coefficiente binomiale, o combinazione, che rappresenta il numero di modi per scegliere $ k $ elementi da un insieme di $ n-1 $ elementi.
$ B_k $ è il numero di Bell già calcolato per insiemi con $ k $ elementi.

Il numero di Bell $ B_n $ conta il numero di modi in cui un insieme di $ n $ elementi può essere partizionato in sottoinsiemi disgiunti.

In alternativa, il numero di Bell posso calcolarlo utilizzando la formula esponenziale di Dobinski:

$$ B_n = \frac{1}{e} \sum_{k=0}^{\infty} \frac{k^n}{k!} $$

In genere, il calcolo manuale viene fatto usando la formula ricorsiva, che mi permette di ottenere $ B_5 = 52 $ per l'insieme $ A = \{ 1, 2, 3, 4, 5 \} $.

Esempio

Provo a calcolare il numero di partizioni dell'insieme A che ha n=5 elementi

$$ A = \{ 1,2,3,4,5 \} $$

Utilizzo la formula ricorsiva

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

Sapendo che n=5

$$ B_5 = \sum_{k=0}^{5-1} \binom{5-1}{k} B_k $$

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k $$

Inizio con $ B_0 = 1 $ come condizione iniziale della formula ricorsiva.

$$ B_0=1 $$

Poi utilizzo la formula per calcolare $ B_1 $:

$$ B_1 = \sum_{k=0}^{0} \binom{0}{k} B_k = \binom{0}{0} B_0 $$

Qui sto sommando solo un termine, perché l'unico $ k $ possibile è 0.

$ \binom{0}{0} = 1 $, perché scegliere 0 elementi da un insieme di 0 elementi può essere fatto in un solo modo.
$ B_0 = 1 $ definito inizialmente.

Quindi:

$$ B_1 = 1 \times 1 = 1 $$

Ora calcoliamo $ B_2 $:

$$ B_2 = \sum_{k=0}^{1} \binom{1}{k} B_k = \binom{1}{0} B_0 + \binom{1}{1} B_1 $$

Calcolo ogni termine:

$ \binom{1}{0} = 1 $, perché c'è un modo di scegliere 0 elementi da 1.
$ \binom{1}{1} = 1 $, perché c'è un modo di scegliere 1 elemento da 1.

Sostituisco i valori di $ B_0 $ e $ B_1 $:

$$ B_2 = 1 \times 1 + 1 \times 1 = 1 + 1 = 2 $$

Passo a calcolare $ B_3 $:

$$ B_3 = \sum_{k=0}^{2} \binom{2}{k} B_k = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 $$

Calcolo ogni combinazione:

$ \binom{2}{0} = 1 $, perché c'è un modo di scegliere 0 elementi da 2.
$ \binom{2}{1} = 2 $, perché ci sono due modi di scegliere 1 elemento da 2.
$ \binom{2}{2} = 1 $, perché c'è un modo di scegliere 2 elementi da 2.

Sostituendo i valori di $ B_0 $, $ B_1 $ e $ B_2 $:

$$ B_3 = 1 \times 1 + 2 \times 1 + 1 \times 2 = 1 + 2 + 2 = 5 $$

Adesso calcolo $ B_4 $:

$$ B_4 = \sum_{k=0}^{3} \binom{3}{k} B_k = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 $$

Calcolo ogni combinazione:

$ \binom{3}{0} = 1 $
$ \binom{3}{1} = 3 $, perché ci sono tre modi di scegliere 1 elemento da 3.
$ \binom{3}{2} = 3 $, perché ci sono tre modi di scegliere 2 elementi da 3.
$ \binom{3}{3} = 1 $

Sostituendo i valori di $ B_0 $, $ B_1 $, $ B_2 $, e $ B_3 $:

$$ B_4 = 1 \times 1 + 3 \times 1 + 3 \times 2 + 1 \times 5 = 1 + 3 + 6 + 5 = 15 $$

Infine, calcolo $ B_5 $:

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k = \binom{4}{0} B_0 + \binom{4}{1} B_1 + \binom{4}{2} B_2 + \binom{4}{3} B_3 + \binom{4}{4} B_4 $$

Calcolo ogni combinazione:

$ \binom{4}{0} = 1 $
$ \binom{4}{1} = 4 $, perché ci sono quattro modi di scegliere 1 elemento da 4.
$ \binom{4}{2} = 6 $, perché ci sono sei modi di scegliere 2 elementi da 4.
$ \binom{4}{3} = 4 $
$ \binom{4}{4} = 1 $

Sostituisco i valori di $ B_0 $, $ B_1 $, $ B_2 $, $ B_3 $, e $ B_4 $:

$$ B_5 = 1 \times 1 + 4 \times 1 + 6 \times 2 + 4 \times 5 + 1 \times 15 = 1 + 4 + 12 + 20 + 15 = 52 $$

Quindi, il numero di Bell è $ B_5 = 52 $.

In conclusione, ci sono 52 partizioni possibili per l'insieme $ A = \{ 1,2,3,4,5 \} $ con 5 elementi, calcolato utilizzando la formula ricorsiva e le combinazioni.

Osservazioni

Alcune osservazioni sulle partizioni

La partizione banale
Ogni insieme X ha una partizione banale uguale all'insieme stesso $$ P(A) = \{ A \} $$
Esempio. Considero l'insieme $$ A = \{ 1,2,3,4,5 \} $$ la partizione banale dell'insieme A è la seguente $$ P(A) = \{ \ \{ 1,2,3,4,5 \} \ \} $$
La partizione di singleton
Ogni insieme X ha una partizione composta da sottoinsiemi con un unico elemento (singleton o singoletti) $$ P(A) = \{ \{ a_1 \} , \{ a_2 \} , ... \} $$
Esempio. Considero l'insieme $$ A = \{ 1,2,3,4,5 \} $$ la partizione di singleton dell'insieme A è la seguente $$ P(A) = \{ \ \{ 1 \} \ , \{ 2 \} \ , \{ 3 \} \ , \{ 4 \} \ , \{ 5 \} \ \} $$

E così via.