Un triangolo ha sempre almeno due angoli acuti

Un triangolo ha sempre almeno due angoli acuti. In altre parole, non può avere più di un angolo retto o più di un angolo ottuso.

Questa proprietà deriva direttamente dalla regola fondamentale secondo cui la somma degli angoli interni di un triangolo è sempre 180°.

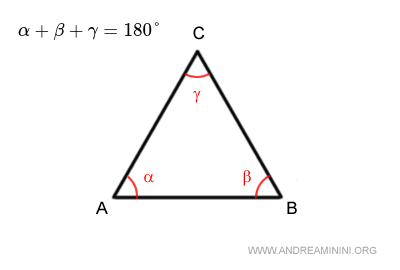
Per dimostrarlo, considero i tre diversi tipi di triangoli:

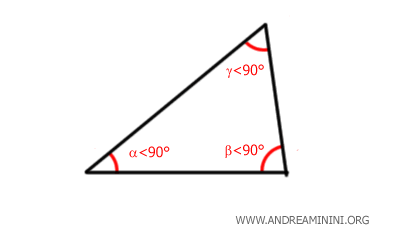
• Triangolo acuto
  Un triangolo acuto ha per definizione tutti gli angoli acuti. Quindi, ha tre angoli acuti.
  
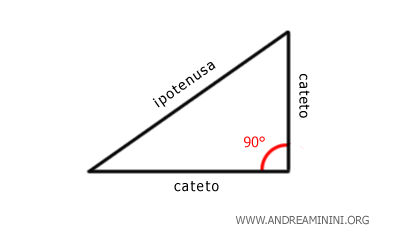
• Triangolo rettangolo
  In questo caso, uno degli angoli misura 90° (angolo retto).  Poiché la somma degli angoli interni deve essere 180°, gli altri due angoli devono necessariamente sommarsi a 90° (ossia \(180° - 90° = 90°\)). Affinché questa somma sia rispettata, ciascuno di questi due angoli deve essere minore di 90°, cioè acuto. Quindi, un triangolo non può avere più di un angolo retto.
  
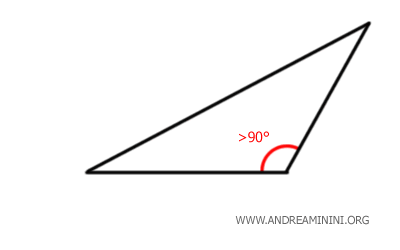
• Triangolo ottusangolo
  In questo caso, il triangolo ha un angolo ottuso, cioè maggiore di 90°.  Dato che la somma totale deve sempre essere 180°, gli altri due angoli devono sommarsi a un valore inferiore a 90° perché \(180° \) meno un angolo ottuso sarà un valore inferiore a 90°. Questo implica che entrambi gli angoli rimanenti devono essere minori di 90°, e quindi acuti. Quindi, un triangolo non può avere più di un angolo ottuso.
  

In conclusione, poiché un triangolo non può mai avere due angoli retti, né due angoli ottusi, almeno due angoli di qualsiasi triangolo devono sempre essere acuti, indipendentemente dal tipo di triangolo che considero.

E così via.