Il teorema del triangolo isoscele
Un triangolo è isoscele se e solo se ha due angoli congruenti alla base del triangolo.
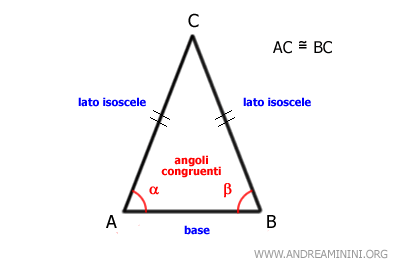
Questo perché in un triangolo, i lati opposti ad angoli uguali sono uguali.
Pertanto, se un triangolo è isoscele allora ha due angoli congruenti.
Vale anche l'inverso del teorema, se un triangolo ha due angoli congruenti, allora è un triangolo isoscele.
In altre parole, gli angoli congruenti alla base sono una condizione necessaria e sufficiente per un triangolo isoscele.
La dimostrazione
Considero un triangolo isoscele.

Per definizione, un triangolo isoscele ha due lati congruenti, ovvero della stessa lunghezza
$$ \overline{AC} \cong \overline{BC} $$
In questo caso sono i lati AC e BC mentre il lato AB è la base del triangolo isoscele.
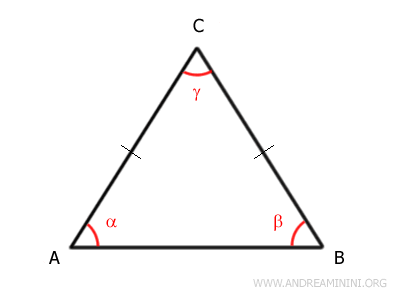
Devo dimostrare che il triangolo ha anche due angoli congruenti alla base.
Traccio la bisettrice CD dell'angolo γ che taglia a metà l'angolo in due, ottenendo due angoli congruent γ1 e γ2.
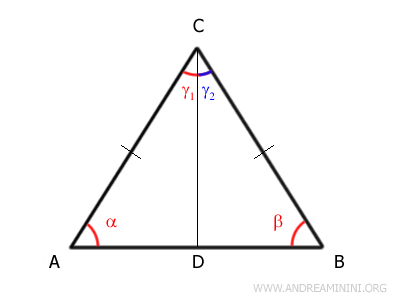
In questo modo ottengo due triangoli rettangolo ACD e BCD.
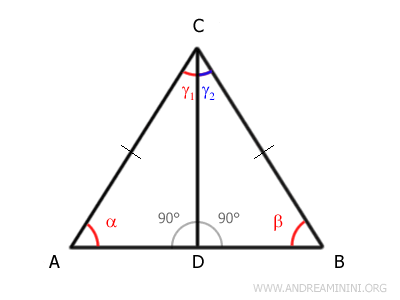
Per il primo principio di congruenza, i triangoli ACD e BCD sono congruenti, perché hanno due lati congruenti CD=CD, AC≅AB e l'angolo tra di essi congruente γ1≅γ2.
- I due triangoli hanno il lato CD in comune $$ \overline{CD} \cong \overline{CD} $$
- I lati AC e BC congruenti perché ABC è un triangolo isoscele per l'ipotesi iniziale $$ \overline{AC} \cong \overline{BC} $$
- Gli angoli γ1 e γ2 sono congruenti, ossia hanno la stessa ampiezza, perché l'angolo γ è stato diviso a metà dalla bisettrie. $$ \gamma_1 \cong \gamma_2 $$
Se i due triangoli ACD e BCD sono congruenti, allora hanno tutti i lati e gli angoli congruenti nello stesso ordine.
Pertanto, gli angoli alfa e beta sono congruenti.
$$ \alpha \cong \beta $$
Questo dimostra che il triangolo isoscele ha gli angoli alla base congruenti.
La dimostrazione inversa
Ora devo dimostrare l'inverso, ossia se un triangolo ha due angoli congruenti alla base, allora è un triangolo isoscele.
Per ipotesi iniziale, considero un triangolo con due angoli congruenti (α≅β)
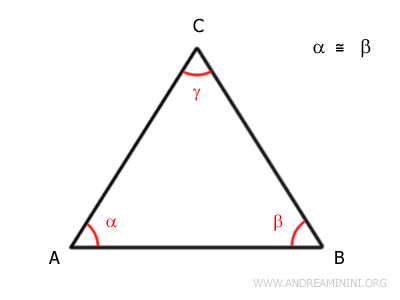
Quindi, per ipotesi iniziale gli angoli alfa e beta sono congruenti.
$$ \alpha \cong \beta $$
Devo dimostrare che il triangolo è isoscele.
Prolungo i lati AC e BC con due segmenti congruenti AD≅BE
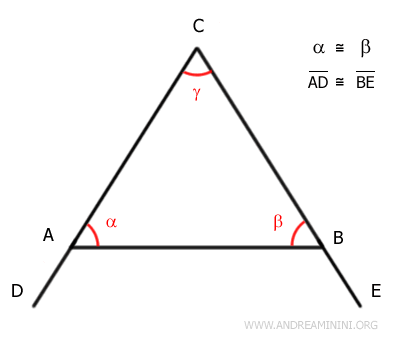
Aggiungo gli angoli α' e β'
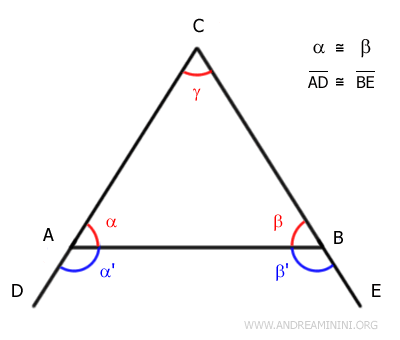
Gli angoli α e α' e gli angoli β e β' sono angoli supplementari perché la loro somma forma un angolo piatto (180°).
$$ \alpha + \alpha ' = 180° $$
$$ \beta + \beta ' = 180° $$
Quindi, posso ricavare gli angoli α' e β' per differenza
$$ \alpha ' = 180° - \alpha $$
$$ \beta ' = 180° - \beta $$
Sapendo che gli angoli α≅β sono congruenti per l'ipotesi iniziale, deduco che anche gli angoli α' e β' sono congruenti, ossia hanno la stessa ampiezza.
$$ \alpha ' = \beta ' $$
A questo punto congiungo il punto A con E e il punto B con D.
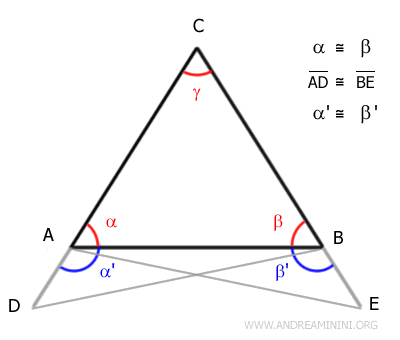
Per il primo criterio di congruenza, i triangoli ABD e ABE sono congruenti perché hanno un lato in comune (AB), i lati AD≅BE congruenti e gli angoli congruenti α'≅β' tra i due lati
$$ ABD \cong ABE $$
Una volta assodato che ABD≅ABE sono congruenti, deduco che tutti i loro lati e angoli sono congruenti nello stesso ordine.
Di questi mi interessa soprattutto la congruenza tra i lati BD≅AE
$$ \overline{BD} = \overline{AE} $$
La congruenza tra gli angoli δ≅ε
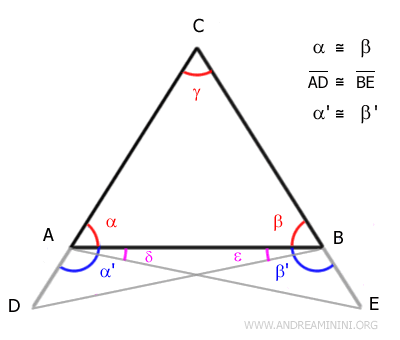
E la congruenza tra gli angoli θ≅σ
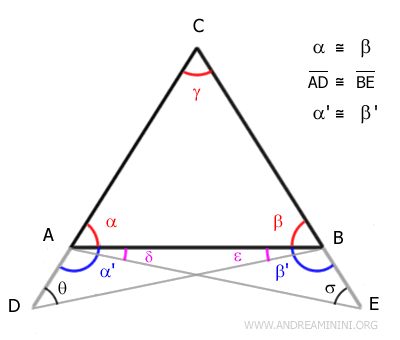
Sapendo che i seguenti angoli sono congruenti
$$ \alpha \cong \beta $$
$$ \delta \cong \epsilon $$
Deduco che sono congruenti anche gli angoli
$$ \alpha + \delta \cong \beta + \epsilon $$
Per il secondo principio di congruenza, questo mi permette di stabilire la congruenza dei triangoli ACE e BCD perché hanno due lati congruenti AE≅BD e due angoli congruenti α+δ≅β+ε e θ≅σ

Di conseguenza, se i triangoli ACE e BCD sono congruenti
$$ ACE \cong BCD $$
Deduco che tutti i loro lati e angoli sono ordinatamente congruenti.
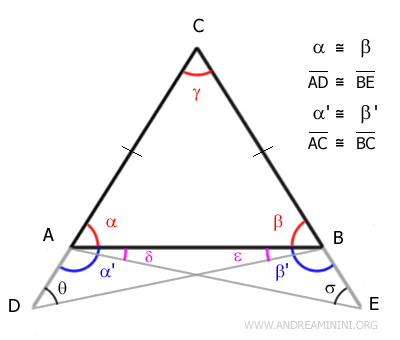
In particolar modo, sono congruenti i lati AC e BC
$$ \overline{AC} \cong \overline{BC} $$
Questo mi permette di affermare che il triangolo ABC è un triangolo isoscele, perché ha due lati congruenti (AC≅BC)
Dimostrazione alternativa
Considero un triangolo con due angoli congruenti, \( \alpha \cong \beta \).

Traccio le bisettrici degli angoli \( \alpha \) e \( \beta \).
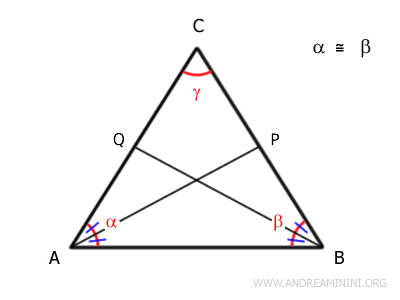
Poiché questi angoli sono congruenti, anche le loro metà lo saranno:
\[ A\widehat{B}Q \cong C\widehat{B}Q \cong B\widehat{A}P \cong C\widehat{A}P \]
I triangoli \( ABQ \) e \( ABP \) risultano congruenti per il secondo criterio di congruenza (angolo-lato-angolo), poiché condividono il lato \( AB \) e hanno gli angoli adiacenti congruenti \( \alpha \cong \beta \) e \( B\widehat{A}P \cong A\widehat{B}Q \).
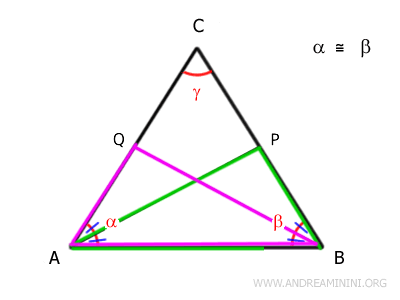
Dalla congruenza dei triangoli \( ABQ \cong ABP \), segue che tutti i loro lati e angoli corrispondenti sono uguali, in particolare \( AP = BQ \) e \( A\widehat{Q}B = B\widehat{P}A \).
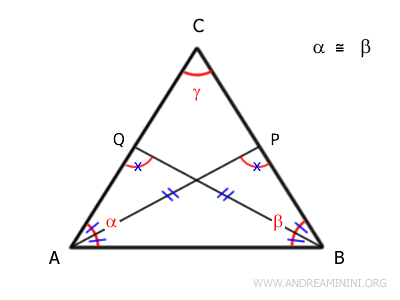
Essendo \( A\widehat{Q}B = B\widehat{P}A \) congruenti, anche i loro angolu supplementari devono esserlo:
\[ C\widehat{P}A = C\widehat{Q}B \]
Ora, considero i triangoli \( APC \) e \( BQC \).
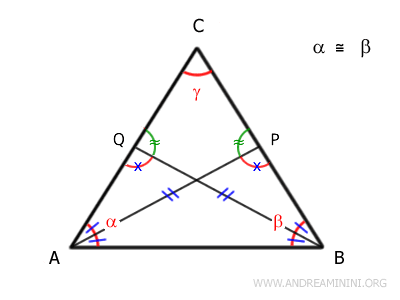
I triangoli \( APC \) e \( BQC \) risultano congruenti per il secondo criterio di congruenza, poiché hanno un lato congruente \( AP = BQ \) (già dimostrato) e gli angoli adiacenti congruenti \( C\widehat{A}P = C\widehat{B}Q \) e \( C\widehat{P}A = C\widehat{Q}B \).
Dalla congruenza dei triangoli \( APC \cong BQC \), segue che tutti i loro lati e angoli corrispondenti sono uguali. In particolare, ottengo:
\[ AC = BC \]
Questo dimostra che il triangolo \( ABC \) è isoscele, poiché ha due lati congruenti.

E così via.
