Area del triangolo
L'area di un triangolo si calcola mediante una formula molto semplice. Se b è la lunghezza della base del triangolo e h è la sua altezza (il segmento perpendicolare tracciato dalla base a un vertice opposto), l'area A del triangolo è data da: $$ A = \frac{b \cdot h}{2} $$
Questa formula deriva dal fatto che un triangolo posso considerarlo come la metà di un parallelogramma che ha la stessa base e la stessa altezza.
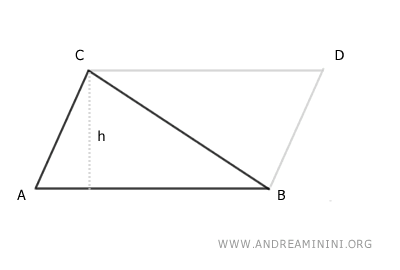
Questa intuizione geometrica è molto utile perché collega proprietà di due figure geometriche diverse.
L'area del parallelogramma è il prodotto base per altezza.
Quindi, l'area del triangolo è il prodotto base per altezza diviso due.
Le formule Inverse
Oltre alla formula base, ci sono anche formule inverse che possono essere utilizzate per determinare la base o l'altezza di un triangolo se si conosce la sua area.
$$ b=\frac{2A}{h} $$
Allo stesso modo posso calcolare l'altro cateto.
$$ h=\frac{2A}{b} $$
Queste formule inverse sono particolarmente utili nella risoluzione dei problemi di geometria.
Un esempio pratico
Prendo come esempio un triangolo scaleno in cui l'altezza è h=7.0588 e la base è c=17
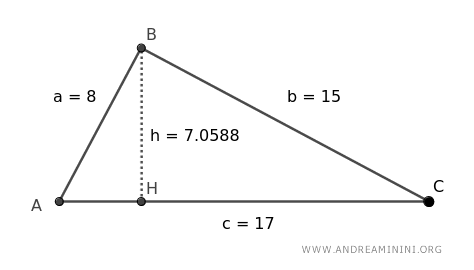
Per calcolare l'area del triangolo calcolo la base per l'altezza
$$ A=\frac{c \cdot h}{2} = \frac{17 \cdot 7.0588}{2} \approx 60 $$
L'area del sito è A=60.
L'area del triangolo rettangolo
Nel caso particolare del triangolo rettangolo, l'area si calcola moltiplicando tra loro i due cateri.
$$ A = \frac{c_1 \cdot c_2}{2} $$
Questo perché un cateto coincide con una base (b=c1) e l'altro con un'atlezza (h=c2) del triangolo, e dividendo il prodotto per due
La formula di Erone
La formula di Erone mi permette di calcolare l'area di qualsiasi triangolo, se conosco solo le lunghezze dei lati.
$$ A = \sqrt{p \cdot (p-l_1) \cdot (p-l_2) \cdot (p-l_2)} $$ Dove \( l_1 \), \( l_2 \), e \( l_3 \) sono i lati e \(p = \frac{l_1+l_2+l_3}{2}\) è il semiperimetro del triangolo.
Questa formula è molto utile quando l'altezza del triangolo non è nota ed è difficile da calcolare.
Esempio
Considero il triangolo dell'esempio precedente.

Provo a calcolare l'area usando la sola conoscenza delle lunghezze dei lati tramite la formula di Erone.
In questo caso i lati sono a=8, b=15, c=17.
$$ A = \sqrt{p \cdot (p-8) \cdot (p-15) \cdot (p-17)} $$
Calcolo il semiperimetro del triangolo.
$$ p = \frac{8+15+17}{2} = \frac{40}{2} = 20 $$
Sostituisco il perimetro p=20 nella formula di Erone.
$$ A = \sqrt{p \cdot (p-8) \cdot (p-15) \cdot (p-17)} $$
$$ A = \sqrt{20 \cdot (20-8) \cdot (20-15) \cdot (20-17)} $$
$$ A = \sqrt{20 \cdot 12 \cdot 5 \cdot 3} $$
$$ A = \sqrt{3600)} $$
$$ A = 60 $$
L'area del triangolo è 60.
E' lo stesso risultato ottenuto nell'esempio precedente.
Area del triangolo con la trigonometria
L'area di un triangolo può essere calcolata anche usando la trigonometria.
L'area del triangolo è il semiprodotto di due lati l1, l2 per il seno dell'angolo (α) compreso tra i due lati. $$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$
Dove l1 e l2 sono due lati adiacenti del triangolo mentre α è l'angolo compreso tra i due lati.
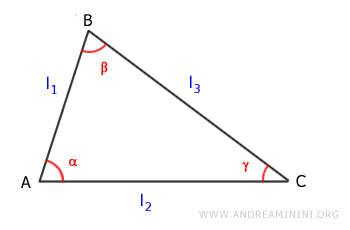
Lo stesso principio posso applicarlo a qualsiasi altro angolo del triangolo con i relativi lati adiacenti.
$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$
$$ Area = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$
Questo principio è applicabile a qualsiasi tipo di rettangolo (isoscele, rettangolo, scaleno).
Esempio
Prendo come esempio un triangolo scaleno con queste misure:
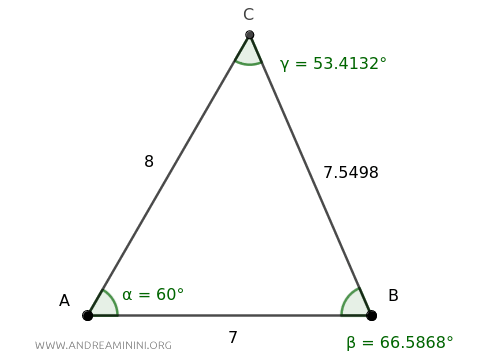
L'angolo α ha un'ampiezza di 60° e i lati adiacenti sono lunghi AB=7 e AC=8.
Per calcolare l'area del triangolo utilizzo la formula
$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$
In questo caso $ \alpha = 60° $, $ l_1 = \overline{AB}=7 $ e $ l_2 = \overline{AC}=8 $
$$ Area = \frac{1}{2} \cdot (7 \cdot 8) \cdot \sin 60° $$
$$ Area = \frac{1}{2} \cdot (56) \cdot \sin 60° $$
$$ Area = 28 \cdot \sin 60° $$
Sapendo che $ \sin 60° = \frac{\sqrt{3}}{2} $
$$ Area = 28 \cdot \frac{\sqrt{3}}{2} $$
$$ Area = 14 \cdot \sqrt{3} $$
$$ Area = 24,2487 $$
Ho così trovato l'area del triangolo ABC usando i principi della trigonometria.
Verifica. Per verificare se il risultato è corretto, misuro un'altezza del triangolo.
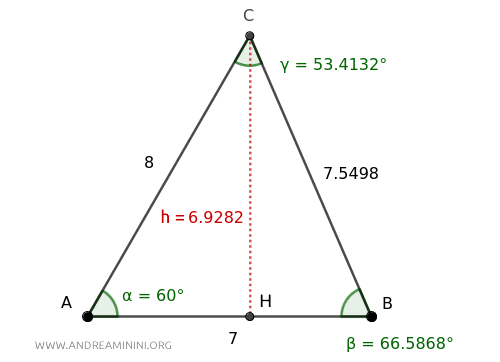
Poi calcolo l'area del triangolo usando la formula geometrica: base per altezza diviso due. $$ Area = \frac{\overline{AB} \cdot h}{2}=\frac{\overline{7} \cdot 6,9282}{2}=24,2487$$ Il risultato è lo stesso. La verifica conferma il risultato già ottenuto con la formula trigonometrica.
E così via.
