Il teorema di Pitagora generalizzato
Dato un triangolo rettangolo e tre poligoni simili costruiti sui lati del triangolo, l'area del poligono costruito sull'ipotenusa è uguale alla somma delle aree dei poligoni costruiti sui cateti.
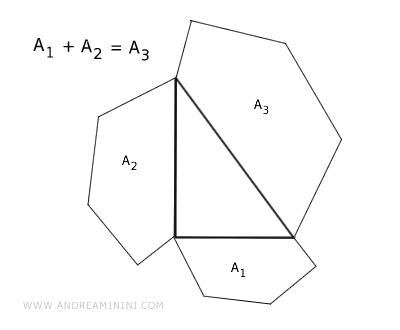
In altre parole, il poligono costruito sull'ipotenusa è equivalente alla somma dei poligoni costruiti sui cateti.
L'estensione di questo teorema, sostiene che la proprietà del triangolo rettangolo descritta nel teorema di Pitagora non si limita ai quadrati ma si applica a qualsiasi figura geometrica simile costruita su quei lati.
Nota. Questo significa che, posso costruire triangoli, cerchi, poligoni regolari o qualsiasi altra forma simile sui tre lati del triangolo rettangolo. L'area totale delle forme costruite sui cateti sarà sempre uguale all'area della forma costruita sull'ipotenusa.
Un esempio
In questo esempio ho un triangolo rettangolo ABC su cui costruisco tre pentagoni regolari.
I cateti del triangolo rettangolo misurano AB=4, AC=3 mentre l'ipotenusa BC=5.
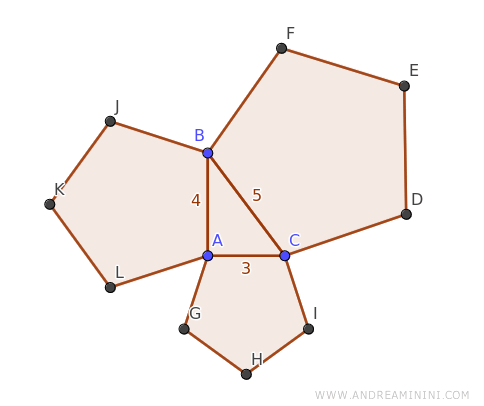
I pentagoni sono poligoni regolari con lo stesso numero di lati, quindi sono anche poligoni simili.
Nota. Il teorema non impone che i poligoni debbano essere regolari. Possono anche essere irregolari, purché siano poligoni simili. In questo esempio ho scelto i poligoni regolari perché diventa molto più semplice il calcolo delle aree. Inoltre, tutti i poligoni regolari con lo stesso numero di lati sono sempre dei poligoni simili.
A questo punto calcolo l'area dei pentagoni.
L'area di un poligono regolare è uguale al semiperimetro (p) moltiplicato per l'apotema (a).
$$ A = p \cdot a $$
In un pentagono l'apotema è il prodotto a=l·f tra un lato e il numero fisso (f) che nel caso dei pentagoni è f=0.688
$$ A = p \cdot ( l \cdot f ) $$
$$ A = p \cdot ( l \cdot 0.688 ) $$
L'area del pentagono costruito sul cateto AB=3 (lato di lunghezza 3) è A1=15.48
$$ A_1 = \frac{3 \cdot 5}{2} \cdot ( 3 \cdot 0.688 ) = 15.48 $$
L'area del pentagono costruito sul cateto AC=4 (lato di lunghezza 4) è A2=27.52
$$ A_2 = \frac{4 \cdot 5}{2} \cdot ( 4 \cdot 0.688 ) = 27.52 $$
L'area del pentagono costruito sull'ipotenusa BC=5 (lato di lunghezza 5) è A2=43
$$ A_2 = \frac{5 \cdot 5}{2} \cdot ( 5 \cdot 0.688 ) = 43 $$
Faccio una rapida verifica con Geogebra per controllare se le aree sono effettivamente giuste:
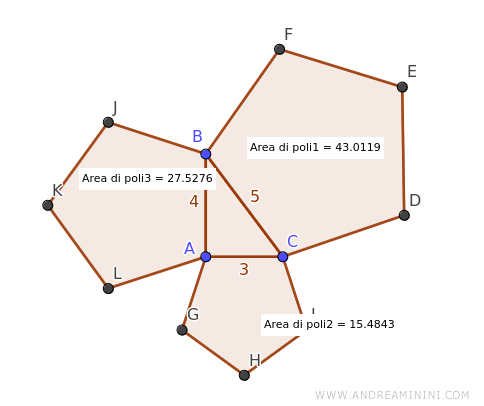
A questo punto verifico se la somma dei pentagoni costruita sui cateti è equivalente al pentagono costruito sull'ipotenusa.
$$ A_1 + A_2 = A_3 $$
Sostituisco A1=15.48, A2=27.52, A2=43
$$ 15.48 + 27.52 = 43 $$
$$ 43 = 43 $$
La somma delle aree dei pentagoni costruiti sui cateti A1+A2 è effettivamente uguale all'area A3 del pentagono simile costruito sull'ipotenusa.
La dimostrazione
Considero un triangolo rettangolo e tre poligoni simili costruiti sui lati del triangolo.
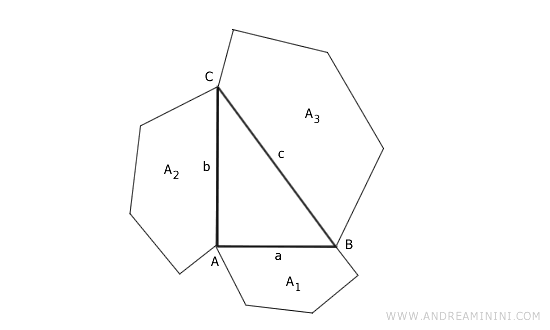
Essendo poligoni simili, secondo il teorema delle aree dei poligoni simili le loro aree sono pari al quadrato dei lati omologhi corrispondenti.
$$ \frac{A_3}{A_2} = ( \frac{c}{b} )^2 $$
Quindi
$$ A_3 = A_2 \cdot ( \frac{c}{b} )^2 $$
$$ A_3 = A_2 \cdot \frac{c^2}{b^2} $$
Sapendo che due poligoni simili hanno i lati proporzionali con lo stesso rapporto di proporzionalità k
$$ k = \frac{a}{b} $$
Per il teorema di Pitagora la somma dei quadrati costruiti sui cateti è uguale al quadrato costruito sull'ipotenusa.
$$ c^2 = a^2 + b^2 $$
Poiché k=a/b deduco che a=kb
$$ c^2 = (kb)^2 + b^2 $$
$$ c^2 = k^2 b^2 + b^2 $$
$$ c^2 = b^2 (k^2 + 1) $$
Quindi, tornando al rapporto delle aree dei poligoni simili posso sostituire c2=b2(k2+1)
$$ A_3 = A_2 \cdot \frac{c^2}{b^2} $$
$$ A_3 = A_2 \cdot \frac{b^2 (k^2 + 1)}{b^2} $$
$$ A_3 = A_2 \cdot (k^2 + 1) $$
A questo punto, per dimostrare che anche la somma A1+A2=A3 devo dimostrare che A1+A2=A2(k2+1)
Sapendo che k=a/b sempre per il teorema delle aree dei poligoni simili deduco che k2 è il rapporto tra le aree dei poligoni simili costruiti sui cateti a e b.
$$ k^2 = \frac{A_1}{A_2} $$
Ovvero
$$ A_1 = k^2 \cdot A_2 $$
Quindi, sapendo che A1=k2A2 posso riscrivere la somma A1+A2 in questo modo
$$ A_1 + A_2 = ( k_2 \cdot A_2 ) + A_2 $$
$$ A_1 + A_2 = A_2 \cdot (k_2 +1 ) $$
Questo dimostra che A1+A2=A3 poiché A1+A2=A2(k2+1) e A3=A2(k2+1)
$$ A_1 + A_2 = A_2 \cdot (k_2 +1 ) = A_3 $$
Pertanto, la somma delle aree dei poligoni simili costruiti sui cateti è uguale all'area del poligono costruito sull'ipotenusa.
$$ A_1 + A_2 = A_3 $$
Ho così dimostrato il teorema.
Dimostrazione alternativa
Prendo in considerazione triangolo rettangolo ABC e tre poligoni simili costruiti sui cateti (a,b) e sull'ipotenusa (c) del triangolo.

Per ipotesi iniziale i poligoni costruiti sui lati del triangolo sono simili.
Quindi, in base al teorema delle aree dei poligoni simili i rapporti delle loro aree sono pari al quadrato del rapporto dei lati omologhi.
$$ \frac{A_1}{A_2} = ( \frac{a}{b} )^2 $$
$$ \frac{A_1}{A_2} = \frac{a^2}{b^2} $$
Questo vuol dire che il rapporto tra le aree dei poligoni simili costruiti sui cateti del triangolo è uguale al rapporto tra i quadrati costruiti sugli stessi cateti.
Indico i quadrati con Q1=a2 e Q2=b2
$$ \frac{A_1}{A_2} = \frac{Q_1}{Q_2} $$
Per la stessa ragione vale anche la proporzione
$$ \frac{A_3}{A_2} = \frac{Q_3}{Q_2} $$
A questo punto mi concentro sulla prima proporzione
$$ \frac{A_1}{A_2} = \frac{Q_1}{Q_2} $$
Applico la proprietà del comporre delle proporzioni
$$ \frac{A_1+A_2}{A_2} = \frac{Q_1+Q_2}{Q_2} $$
Per il teorema di Pitagora la somma dei quadrati costruiti sull'ipotenusa Q1+Q2=Q3 è uguale al quadrato costruito sull'ipotenusa.
$$ \frac{A_1+A_2}{A_2} = \frac{Q_3}{Q_2} $$
Sapendo che A3/A2=Q3/Q2
$$ \frac{A_1+A_2}{A_2} = \frac{A_3}{A_2} $$
Semplifico e ottengo
$$ A_1 + A_2 = A_3 $$
Questo dimostra che la somma delle aree dei poligoni simili costruiti sui cateti del triangolo rettangolo è uguale all'area del poligono simile costruito sull'ipotenusa.
E così via.
