Teorema delle aree dei poligoni simili

In due poligoni simili il rapporto tra le aree è uguale al quadrato del rapporto di similitudine $ \frac{A}{A'} = k^2 $

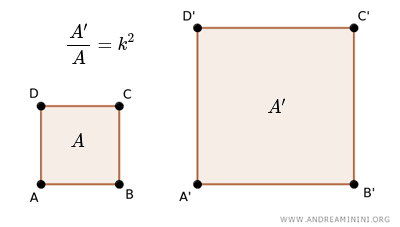
Detto in altri termini, in due poligoni simili il rapporto tra le superfici è il quadrato del rapporto tra i lati omologhi.

$$ \frac{A'}{A} = k^2 = ( \frac{ l }{ l' } )^2 $$

Dove k è il fattore di similitudine e l, l′ sono le lunghezze dei lati corrispondenti nei due poligoni simili.

La formula precedente indica che se un poligono ha una dimensione k volte quella di un altro poligono simile, allora l'area del poligono più grande è k² volte l'area del poligono più piccolo.

$$ A' = A \cdot k^2 $$

Per questa ragione le aree, che sono grandezze bidimensionali, aumentano o diminuiscono con il quadrato del fattore di scala, da qui la relazione k².

Ad esempio, considero due quadrati in cui il lato di uno è il doppio rispetto all'altro. In questo caso, la superficie del quadrato più grande sarà quattro volte quella del quadrato più piccolo.

Un esempio pratico

In questo esempio prendo due quadrati simili.

Il primo quadrato ogni un lato di lunghezza 2 mentre il secondo ha ogni lato di lunghezza 4.

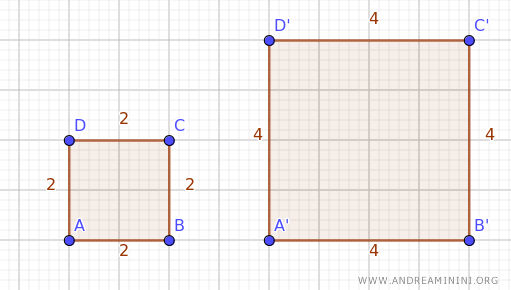
Il rapporto di similitudine tra i due quadrati è k=2, ovvero un quadrato ha il doppio del lato dell'altro.

$$ k = \frac{ \overline{A'B'} }{ \overline{AB} }= \frac{4}{2} = 2 $$

Calcolo l'area dei due quadrati.

$$ A = \overline{AB} \cdot \overline{BC} = 2 \cdot 2 = 4 $$

$$ A' = \overline{A'B'} \cdot \overline{B'C'} = 4 \cdot 4 = 16 $$

L'area del secondo quadrato, quello più grande, è il quadrato dell'area del primo quadrato.

La dimostrazione

Prendo in considerazione due poligoni simili. Ad esempio, due quadrati simili.

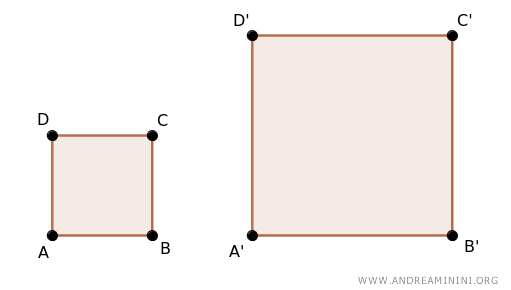
Essendo poligoni simili hanno tutti i lati proporzionali con lo stesso rapporto di similitudine k.

$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = k $$

Considero il segmento AB la base (b) e il segmento BC l'altezza (h) del poligono.

$$ \frac{ \overline{b'} }{ \overline{b} } = \frac{ \overline{h'} }{ \overline{h} } = k $$

Questo vuol dire che

$$ \frac{ \overline{b'} }{ \overline{b} } =  k $$

$$ \frac{ \overline{h'} }{ \overline{h} } =  k $$

Da queste ultime equazioni ricavo b' e h' dal resto.

$$ b' = k \cdot b $$

$$ h' = k \cdot h $$

A questo punto calcolo l'area del secondo quadrato

$$ A' = b' \cdot h' $$

Sapendo che b'=kb e h'=kh li sostituisco

$$ A' = (b \cdot k) \cdot (h \cdot k) $$

$$ A' = b \cdot h \cdot k^2 $$

Il prodotto base per altezza A=b·h è l'area del primo quadrato

$$ A' = A \cdot k^2 $$

Questo dimostra che il rapporto tra le aree dei poligoni simili è uguale al quadrato del rapporto di similitudine

$$ \frac{ A' }{A} = k^2 $$

E questo vale per qualsiasi poligono, non solo per i quadrati. Se i poligoni fossero stati due triangoli o altro, il ragionamento logico sarebbe stato lo stesso.

E così via.