Triangolo isoscele

Il triangolo isoscele è un tipo di triangolo che ha due lati congruenti, ossia della stessa lunghezza, chiamati lati isosceli o lati obliqui.

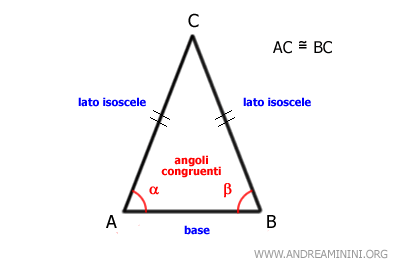
Il terzo lato del triangolo isoscele è la base del triangolo.

I due lati congruenti creano due angoli alla base che sono anch'essi uguali o congruenti.

L'angolo non adiacente alla base (opposto alla base) è detto angolo al vertice.

Perché si chiama isoscele? Il termine "isoscele" deriva dal greco antico. È composto da due parti: "isos", che significa "uguale", e "skelos", che significa "gamba". Quindi, "isoscele" si traduce letteralmente come "gambe uguali", che è una descrizione accurata di questa forma geometrica: un triangolo con due lati (o "gambe") di lunghezza uguale.

Un esempio pratico

Considero questo triangolo ABC.

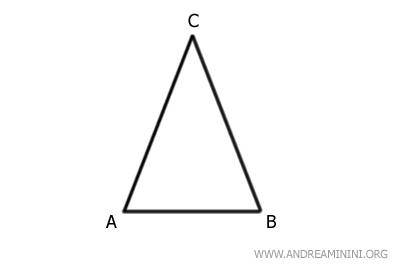
I lati AC e BC sono congruenti perché hanno la stessa lunghezza.

Sono detti "lati isosceli" o "lati obliqui" del triangolo.

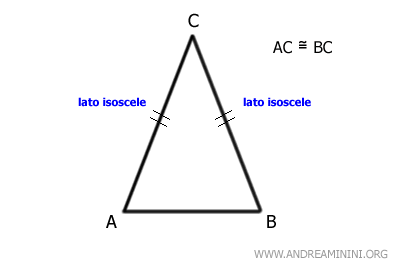
Pertanto, il lato AB non congruente è la base del triangolo.

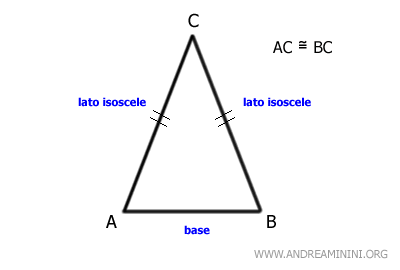
I due lati isosceli formano due angoli congruenti, ossia di pari ampiezza, adiacenti alla base.

Questi angoli sono anche detti "angoli alla base".

Il triangolo isoscele ABC può anche essere detto "triangolo isoscele con vertice C".

Osservazioni

Alcune osservazioni e proprietà dei triangoli isoscele.

• Un triangolo isoscele ha due lati congruenti (AC≅BC)
  

  

• Il teorema del triangolo isoscele

  Un triangolo isoscele se e solo se ha due angoli congruenti ( α≅β).

  Questo perché in un triangolo, i lati opposti ad angoli congruenti sono congruenti.
  

  Nota. In altre parole, se un triangolo ha due angoli congruenti allora è un triangolo isoscele. Inoltre, vale anche il teorema inverso. Se un triangolo è isoscele, allora ha ha due angoli congruenti.

• Gli angoli alla base del triangolo isoscele sono sempre angoli acuti
  
  Gli angoli alla base del triangolo isoscele devono essere due angoli acuti perché, essendo congruenti, non possono essere entrambi angoli retti o ottusi, in quanto un triangolo non può avere più di un angolo retto o più un angolo ottuso.
  

  Spiegazione. Se gli angoli alla base fossero entrambi retti o ottusi, questo violerebbe il teorema della somma di due angoli interni inferiore a 180° da cui deriva la regola che un triangolo ha sempre almeno due angoli interni acuti. Pertanto, se due angoli interni del triangolo sono sempre acuti, qualsiasi triangolo non può avere più di un angolo retto o più di angolo ottuso.

• La bisettrice in un triangolo isoscele

  In un triangolo isoscele la bisettrice dell'angolo opposto alla base coincide con la mediana, l'altezza e l'asse della base.

  
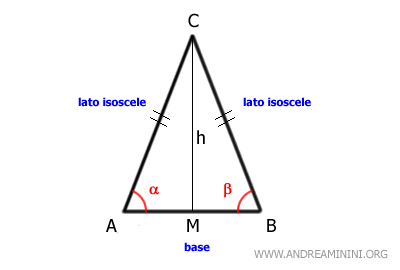
  L'altezza (h) del triangolo isoscele dal vertice alla base crea due triangoli rettangoli congruenti (AMC≅BCM) e divide la base in due segmenti di uguale lunghezza (AM≅BM).
• Un triangolo equilatero è un particolare tipo di triangolo isoscele in cui tutti e tre i lati sono uguali in lunghezza, ossia congruenti. Pertanto, un triangolo equilatero è anche isoscele ma non è detto il contrario. In un triangolo equilatero ciascuno dei suoi lati può essere considerato come base. Inoltre, ha tre angoli congruenti ampi 60°.
  
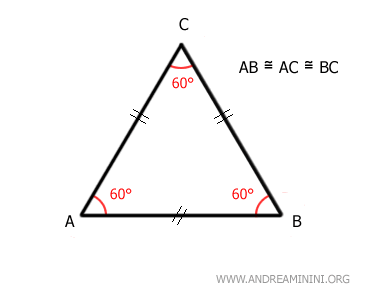
• La somma degli angoli interni di qualsiasi triangolo, compreso l'isoscele, è sempre 180 gradi.
• Un triangolo isoscele può essere acutangolo, rettangolo oppure ottusangolo.
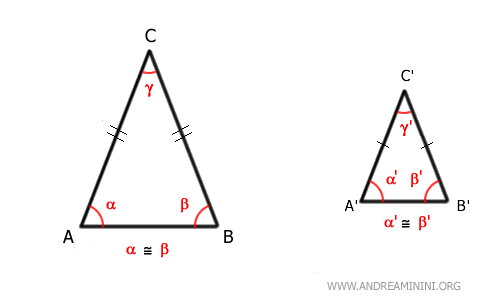
• Due triangoli isosceli sono simili se hanno l'angolo al vertice congruente
  Due triangoli isosceli sono considerati triangoli simili se hanno lo stesso angolo al vertice, cioè l'angolo compreso tra i lati uguali. Questo perché, in ogni triangolo, la somma degli angoli interni è sempre uguale a un angolo piatto (180 gradi). Se gli angoli al vertice γ≅γ' sono congruenti, gli angoli alla base di entrambi i triangoli hanno tutti un'ampiezza uguale a (180°- γ)/2. Di conseguenza, i due triangoli hanno tutti gli angoli congruenti e, in base al primo criterio di similitudine dei triangoli, sono triangoli simili ovvero hanno la stessa forma ma dimensioni che possono essere anche diverse.
  

E così via.