Angoli associati
Gli angoli associati sono angoli espressi in radianti che hanno lo stesso valore delle funzioni goniometriche sotto modulo (valore assoluto). Sono anche detti archi associati.
Un esempio pratico
Il seno dell'angolo α è uguale al modulo del seno di -α.
$$ \sin(\alpha) = | \sin(-\alpha) | $$
Quindi, gli angoli α e -α sono angoli associati per la funzione seno perché restituiscono lo stesso valore assoluto.
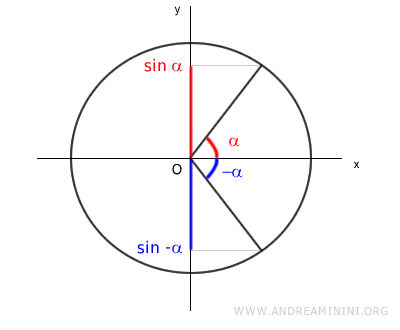
Sapendo che la funzione seno è una funzione dispari f(-x) = -f(x) posso calcolare il valore del seno di -α anche usando l'angolo associato α.
$$ \sin(-\alpha) = - \sin ( \alpha) $$
Nota. Gli angoli α e -α sono angoli associati anche per la funzione coseno. $$ \cos(\alpha) = | \cos(-\alpha) | $$ Entrambe le funzioni restituiscono lo stesso valore assoluto del coseno.
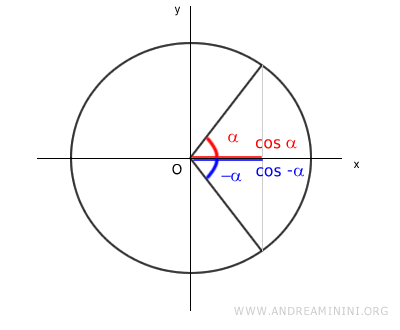
Sapendo che il coseno è una funzione pari f(-x)=f(x), il valore del coseno di -α posso ottenerlo anche usando l'angolo associato $$ \cos( \alpha) = \cos( - \alpha) $$
A cosa servono?
In trigonometria gli angoli associati mi permettono di ridurre al primo quadrante (0 ; π/2) le funzioni goniometriche con un argomento negli altri quadranti (π/2 ; 2π).
La riduzione al primo quadrante semplifica i calcoli.
Esempio. Devo calcolare il coseno di -20°. $$ \cos(-20°) $$ Quest'angolo orientato si trova nel IV quadrante. Sapendo che il coseno ha lo stesso valore per gli angoli opposti, posso ricondurre la formula al primo quadrante. $$ \cos(-20°) = \cos(20°) $$
Le formule degli angoli associati
Ecco le principali formule degli angoli associati in trigonometria.
| Angoli associati | Formule | Dimostrazione |
|---|---|---|
| $$ \alpha \ \ , \ \ - \alpha $$ | $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \pi + \alpha $$ | $$ \sin(\pi+\alpha) = -\sin(\alpha) $$ $$ \cos(\pi+\alpha) = - \cos(\alpha) $$ $$ \tan(\pi+\alpha) = \tan(\alpha) $$ $$ \cot(\pi+\alpha) = \cot(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \pi - \alpha $$ | $$ \sin(\pi-\alpha) = \sin(\alpha) $$ $$ \cos(\pi-\alpha) = - \cos(\alpha) $$ $$ - \tan(\pi-\alpha) = \tan(\alpha) $$ $$ - \cot(\pi-\alpha) = \cot(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ 2 \pi - \alpha $$ | $$ \sin(2 \pi-\alpha) = - \sin(\alpha) $$ $$ \cos(2 \pi-\alpha) = \cos(\alpha) $$ $$ - \tan(2 \pi-\alpha) = \tan(\alpha) $$ $$ - \cot(2 \pi-\alpha) = \cot(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \frac{ \pi }{2} + \alpha $$ | $$ \sin( \frac{ \pi }{2} + \alpha) = \cos(\alpha) $$ $$ \cos( \frac{ \pi }{2} + \alpha) = -\sin(\alpha) $$ $$ \tan( \frac{ \pi }{2} + \alpha) = - \cot(\alpha) $$ $$ \cot( \frac{ \pi }{2} + \alpha) = - \tan(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \frac{ \pi }{2} - \alpha $$ | $$ \sin( \frac{ \pi }{2} - \alpha) = \cos(\alpha) $$ $$ \cos( \frac{ \pi }{2} - \alpha) = \sin(\alpha) $$ $$ \tan( \frac{ \pi }{2} - \alpha) = \cot(\alpha) $$ $$ \cot( \frac{ \pi }{2} - \alpha) = \tan(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \frac{3 \pi }{2} + \alpha $$ | $$ \sin( \frac{3 \pi }{2} + \alpha ) = - \cos(\alpha) $$ $$ \cos( \frac{3 \pi }{2} + \alpha ) = \sin(\alpha) $$ $$ \tan( \frac{3 \pi }{2} + \alpha ) = - \cot(\alpha) $$ $$ \cot( \frac{3 \pi }{2} + \alpha ) = - \tan(\alpha) $$ | vedi spiegazione |
| $$ \alpha \ \ , \ \ \frac{3 \pi }{2} - \alpha $$ | $$ \sin( \frac{3 \pi }{2} - \alpha ) = - \cos(\alpha) $$ $$ \cos( \frac{3 \pi }{2} - \alpha ) = - \sin(\alpha) $$ $$ \tan( \frac{3 \pi }{2} - \alpha ) = \cot(\alpha) $$ $$ \cot( \frac{3 \pi }{2} - \alpha ) = \tan(\alpha) $$ | vedi spiegazione |
E così via.
