Funzioni trigonometriche
Le funzioni trigonometriche mettono in relazione l'ampiezza dell'angolo con la lunghezza dei segmenti proiettati sugli assi.
A un angolo di ampiezza α corrisponde uno e un solo punto P sulla circonferenza, individuato dall'intersezione con il raggio.
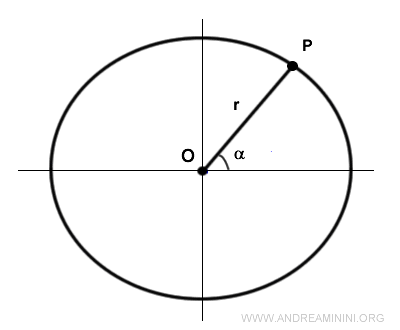
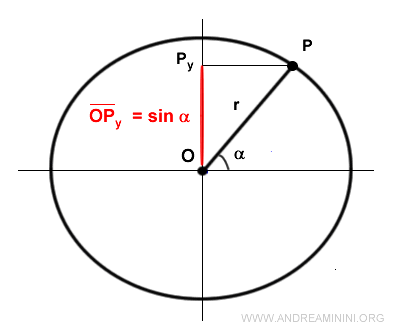
La proiezione del punto P sull'asse delle ordinate individua un segmento OPy detto seno.
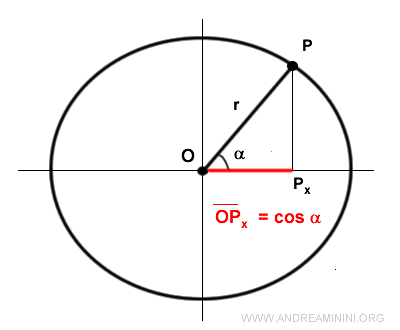
La proiezione del punto P sull'asse delle ascisse individua un segmento OPx detto coseno.
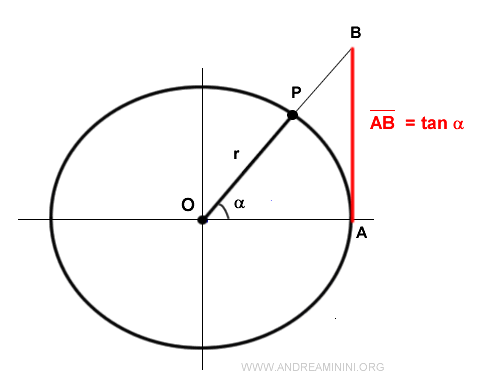
Altri esempi di funzioni trigonometriche sono la tangente e la cotangente.
Gli angoli fondamentali
Ecco alcuni angoli importanti delle funzioni seno e coseno
| angolo (gradi) | angolo (radianti) | seno | coseno | tangente | cotangente |
|---|---|---|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{\sqrt{3}}{3} $$ | $$ \sqrt{3} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ 1 $$ | $$ 1 $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{1}{2} $$ | $$ \sqrt{3} $$ | $$ \frac{\sqrt{3}}{3} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
Il coseno è una funzione periodica di periodo 2π.
Il periodo delle funzioni goniometriche
Le funzioni goniometriche sono funzioni periodiche.
Alcune funzioni hanno lo stesso periodo.
| Funzione | Periodo |
|---|---|
| $$ \sin x $$ | $$ 2 \pi $$ |
| $$ \cos x $$ | $$ 2 \pi $$ |
| $$ \sin (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \cos (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \tan x $$ | $$ \pi $$ |
| $$ \cot x $$ | $$ \pi $$ |
| $$ \tan (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
| $$ \cot (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
E così via.
