La funzione arcoseno
Cos'è l'arcoseno
L'arcoseno è la funzione goniometrica inversa del seno nell'intervallo [-π/2,+π/2]. $$ arcsin $$ Si indica con il simbolo arcsen o arcsin.
A volte l'arcoseno è indicato anche con il simbolo sin-1 dove -1 non indica un esponente ma il simbolo matematico delle funzioni inverse.
Per evitare fraintendimenti è preferibile usare arcsin.
Come funziona l'arcoseno
A partire dal valore y del seno, l'arcoseno calcola l'angolo x in radianti che lo determina.
Esempio
Il seno della funzione vale 0.75
$$ sin \: x = 0.75 $$
Quale angolazione x determina questo valore del seno?
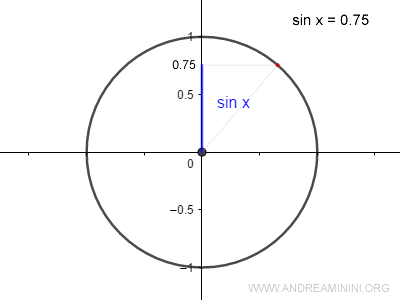
Per saperlo calcolo l'arcoseno del seno.
$$ x = arcsin (0.75) = 0.848 $$
L'arcoseno individua la lunghezza x dell'arco sulla circonferenza determinato dal seno.
L'arco è misurato in radianti e ha la stessa ampiezza dell'angolo x che determina il seno.
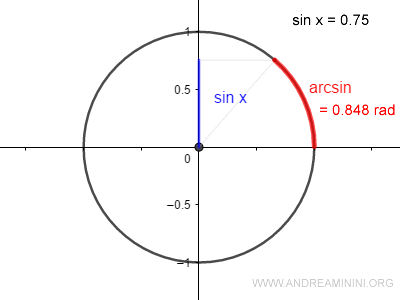
La funzione sin x è uguale a 0.75 quando l'angolo x è uguale a 0.848 radianti.
La dimostrazione
La funzione seno assume valori compresi tra -1 e +1.
Essendo una funzione periodica, lo stesso valore di sin(x) può essere ottenuto da diversi valori di x, ossia da diversi angoli.
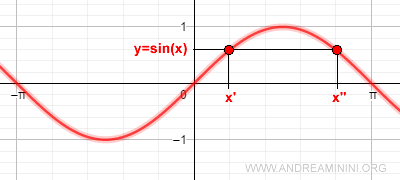
E' quindi impossibile costruire una funzione inversa del seno su tutto il dominio di x perché si viola il principio dell'unicità del valore x rispetto a y=f(x).
$$ f:x -> y $$
Come si costruisce la funzione inversa del seno?
A questo problema c'è una soluzione.
Prendendo in considerazione soltanto una parte del dominio della funzione seno, è possibile soddisfare l'unicità della x.
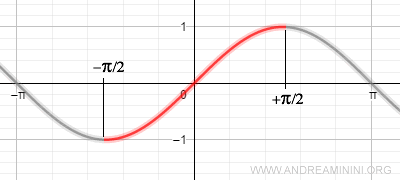
La restrizione del dominio nell'intervallo [-π/2,+π/2] mi permette di ottenere una corrispondenza tra il valore del seno [-1,+1] e il valore della variabile x.
In questo intervallo la funzione seno è biettiva e dunque invertibile.
E' quindi possibile costruire la funzione inversa del seno.
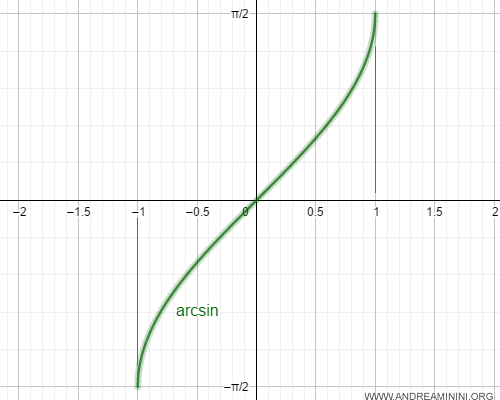
Questa funzione è detta arcoseno.
$$ arcsin(x) : [-1,1] → [-π/2,π/2] $$
L'arcoseno è indicato con la notazione arcsin.
A partire dal valore del seno, la funzione arcoseno calcola l'angolo x che lo determina nell'intervallo [-π/2,π/2]
Nota. L'intervallo [-π/2,π/2] non è l'unico in cui la funzione seno diventa invertibile. Ad esempio, posso invertire la funzione seno anche nell'intervallo [π/2,3π/2] e in infiniti altri intervalli in cui la funzione seno è biettiva.
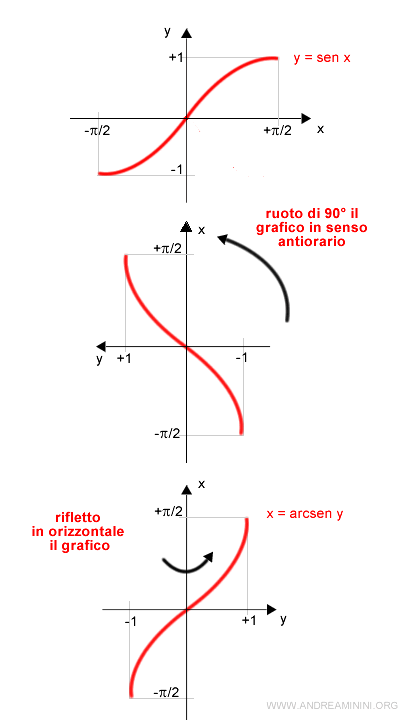
Come costruire il grafico della funzione arcoseno
Posso ottenere il grafico dell'arcoseno a partire dal grafico del seno nel dominio ridotto [-π/2,π/2] tramite due passaggi:
- ruoto di 90° il grafico del seno in senso antiorario
- rifletto in orizzontale il grafico
Il risultato finale è il grafico dell'arcoseno.
Allo stesso modo posso ottenere il grafico dell'arcoseno prendendo in considerazione altri domini ridotti.
Ad esempio, [π/2,3π/2] o altri intervalli in cui il seno è una funzione invertibile.
E così via.
