Cosa sono i radianti
In una circonferenza goniometrica il radiante è l'angolo determinato da un arco di lunghezza uguale al raggio.
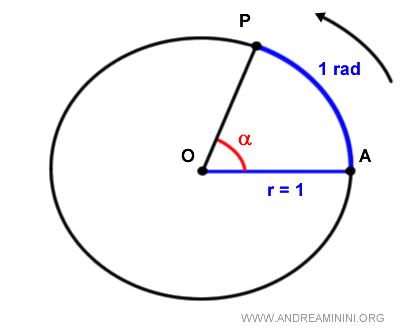
Un radiante misura circa 57,3° gradi nel sistema sessagesimale.
I radianti sono l'unità di misura dell'ampiezza degli angoli.
Si indicano con il simbolo rad.
Nota. Esistono altre unità di misura dell'ampiezza degli angoli. Se non specificato si intende la misura in radianti anche se manca il simbolo rad.
Dimostrazione
Prendo in considerazione lo stesso angolo α in due circonferenze che hanno un raggio diverso r e r'.
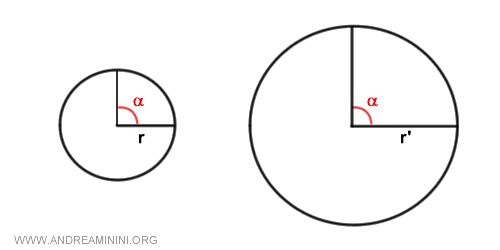
Se misurassi l'ampiezza degli angoli con la lunghezza dell'arco avrei due lunghezze diverse.
A parità di angolo, la seconda circonferenza ha un arco più lungo (k'>k) rispetto alla prima circonferenza.
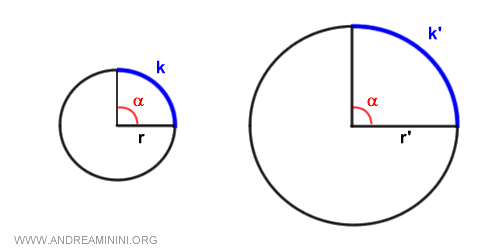
Secondo la proporzionalità tra angoli e archi.
$$ k \ : \ \alpha = 2 \pi r : 360° $$
$$ k' \ : \ \alpha = 2 \pi r' : 360° $$
ossia
$$ \frac{k}{ \alpha} = \frac{2 \pi r}{ 360°} $$
$$ \frac{k'}{ \alpha} = \frac{2 \pi r'}{ 360°} $$
Metto in evidenza la lunghezza degli archi
$$ k = \frac{2 \pi r \cdot \alpha}{ 360°} $$
$$ k'= \frac{2 \pi r' \cdot \alpha }{ 360°} $$
E semplifico 2 e 360
$$ k = \frac{ \pi r \ \alpha}{ 180°} $$
$$ k'= \frac{ \pi r' \alpha}{ 180°} $$
Divido membro a membro
$$ \frac{k}{k'} = \frac{ \frac{ \pi r \alpha}{ 180°} }{ \frac{ \pi r' \alpha}{ 180°} } $$
$$ \frac{k}{k'} =\frac{ \pi r \alpha}{ 180°} \cdot \frac{ 180° }{ \pi r' \alpha } $$
$$ \frac{k}{k'} =\frac{r}{ r'} $$
Sposto a sinistra le grandezze della prima circonferenza e a destra quelle della seconda circonferenza
$$ \frac{k}{r} =\frac{k'}{ r'} $$
Mi accorgo che c'è la stessa proporzione tra la lunghezza dell'arco e del raggio nelle due circonferenze.
$$ k \ : \ r = k' \ : \ r' $$
Questo vuol dire il rapporto tra arco e raggio (k/l) non cambia con le dimensioni della circonferenza.
Pertanto, il rapporto k/l è una buona unità di misura dell'ampiezza dell'angolo perché è generale, mi permette di confrontare tra loro anche angoli di circonferenze con raggio diverso.
$$ \alpha = \frac{k}{r} $$
Il rapporto k/l è detto radiante (rad) ed è pari a 1 quando la lunghezza dell'arco k è uguale alla lunghezza del raggio r.

La misura dei principali angoli in radianti e grado
In questa tabella sono riassunte le principali misure degli angoli in radianti e in gradi
| gradi | radianti |
|---|---|
| 0° | 0 |
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 120° | 2/3 π |
| 135° | 3/4 π |
| 150° | 5/6 π |
| 180° | π |
| 270° | 3/2 π |
| 360° | 2 π |
Come ricordarle tutte? Inizialmente è un aspetto che può mettere in difficoltà. Tuttavia, basta ricordarsi che $$ 15° = \frac{π}{12} \ rad $$ per ricostruire tutte le altre $$ 30° = 2 \cdot 15° = 2 \cdot \frac{π}{12} = \frac{π}{6} \ rad $$ $$ 45° = 3 \cdot 15° = 3 \cdot \frac{π}{12} = \frac{π}{4} \ rad $$ $$ 60° = 4 \cdot 15° = 4 \cdot \frac{π}{12} = \frac{π}{3} \ rad $$ $$ 90° = 6 \cdot 15° = 6 \cdot \frac{π}{12} = \frac{π}{2} \ rad $$ In alternativa, per calcoli più precisi basta ricordarsi che 1° equivale a $$ 1° = \frac{2\pi}{360} = \frac{\pi}{180} \ rad $$ E via dicendo
Perché l'angolo giro è 2π radianti?
Prendo in considerazione l'intera circonferenza, ossia un angolo giro di 360°.
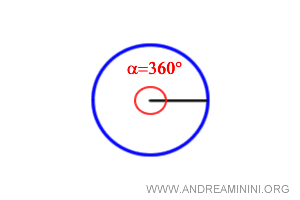
Dalla geometria so già che la lunghezza di una circonferenza è uguale al raggio r per 2 pi greco (π)
$$ k = 2 \pi r $$
Nota la lunghezza della circonferenza (k) e del raggio (r) posso calcolare l'angolo in radianti (rad) è
$$ \alpha = \frac{k}{r} \ rad $$
Sostituisco k con 2πr e ottengo
$$ \alpha = \frac{2 \pi r}{r} \ rad $$
Semplifico e ottengo la misura della circonferenza in radianti.
$$ \alpha = 2 \pi \ rad $$
Sapendo che pi greco (π) è uguale a 3.14
$$ \alpha = 2 \cdot 3.14 \ rad = 6.28 \ rad $$
In conclusione, l'angolo giro (360°) misura 2π radianti ossia 6.28 radianti.
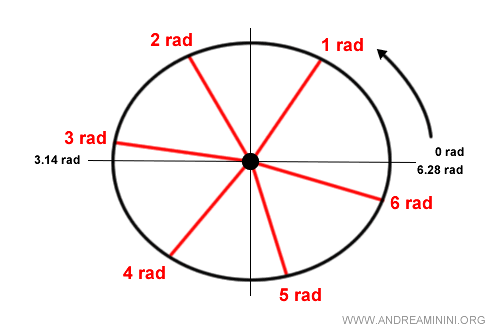
Nota. Se un angolo giro (360°) è pari a 2π radianti, l'angolo piatto (180°) è π radianti ossia 3.14 radianti, perché è. esattamente pari alla metà. A sua volta l'angolo retto (90°) è π/2 radianti. E via dicendo.
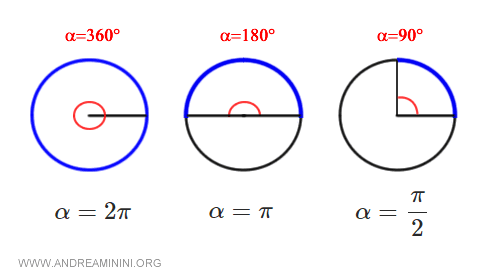
E così via.
