Angoli associati α e π+α
In trigonometria gli angoli associati alfa (α) e π+α mi consentono di utilizzare le seguenti formule di trasformazione. $$ \sin(\pi+\alpha) = -\sin(\alpha) $$ $$ \cos(\pi+\alpha) = - \cos(\alpha) $$ $$ \tan(\pi+\alpha) = \tan(\alpha) $$ $$ \cot(\pi+\alpha) = \cot(\alpha) $$
Essendo angoli associati gli angoli α e π+α hanno lo stesso valore assoluto delle funzioni trigonometriche (seno, coseno, tangente e cotangente).
Dimostrazione e spiegazione
Considero un angolo α e l'angolo π+α su una circonferenza goniometrica.
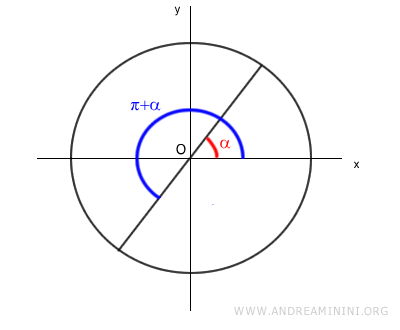
Gli angoli α e π+α differiscono tra loro di un angolo piatto 180° (π).
$$ (\pi + \alpha) - \alpha = \pi $$
Ora costruisco due triangoli rettangolo OAB e OCD.
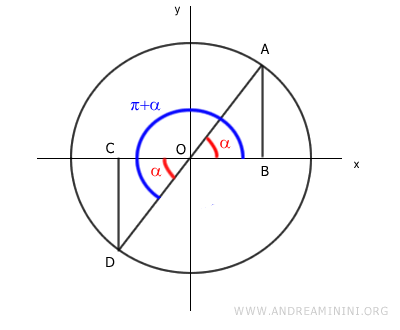
I due triangoli rettangolo OAB e OCD sono congruenti (uguali) perché hanno la stessa ipotenusa (OA=OC) e lo stesso angolo acuto (α) e ovviamente anche un angolo retto (90°).
Quindi, i due triangoli hanno gli stessi angoli e le stesse lunghezze.
Pertanto, i due angoli α e π+α hanno lo stesso valore assoluto del seno perché le altezze dei due triangoli sono uguali AB = CD.
$$ \sin \alpha = | \sin (\pi + \alpha) | $$
Dal punto di vista grafico.
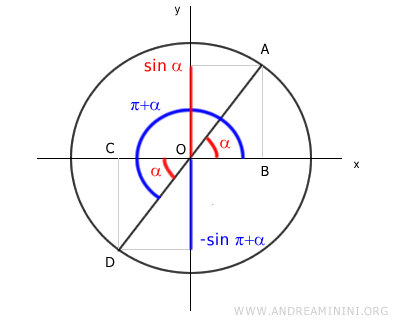
Tuttavia, il segmento AB si trova sulle ordinate positive mentre CD sulle ordinate negative.
Pertanto, il seno degli angoli associati α e π+α ha valore opposto.
$$ \sin \alpha = - \sin (\pi + \alpha) $$
Nota. Moltiplicando entrambi i membri dell'equazione per -1 ottengo anche la relazione opposta $$ (-1) \cdot \sin \alpha = (-1) \cdot (- \sin (\pi + \alpha)) $$ $$ - \sin \alpha = \sin (\pi + \alpha) $$
I due angoli α e π+α hanno lo stesso valore assoluto del coseno (OB=OD).
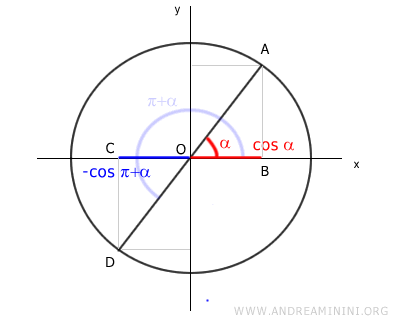
Anche in questo caso il valore del coseno è opposto, perché il segmento OC si trova sulle ascisse negative mentre OB sulle ascisse positive.
$$ \cos \alpha = - \cos (\pi + \alpha) $$
Nota. Moltiplicando entrambi i membri dell'equazione per -1 ottengo anche la relazione opposta $$ (-1) \cdot \cos \alpha = (-1) \cdot ( - \cos (\pi + \alpha) ) $$ $$ - \cos \alpha = \cos (\pi + \alpha) $$
Pertanto, il coseno degli angoli associati α e π+α ha valore opposto.
A questo punto posso ottenere indirettamente le formule di trasformazione della tangente e della cotangente.
La tangente è il rapporto tra il seno e il coseno.
$$ \tan ( \pi + \alpha ) = \frac{ \sin (\pi + \alpha) }{ \cos (\pi + \alpha) } $$
Sapendo che sin(π+α) = - sin(α) e cos(π+α) = - cos(α)
$$ \tan ( \pi + \alpha ) = \frac{ \sin (\pi + \alpha) }{ \cos (\pi + \alpha) } = \frac{ - \sin \alpha }{ - \cos \alpha } = \tan \alpha $$
Quindi, la tangente dell'angolo π+α è uguale alla tangente di α.
La cotangente è il rapporto tra il coseno e il seno.
$$ \cot ( \pi + \alpha ) = \frac{ \cos (\pi + \alpha) }{ \sin (\pi + \alpha) } $$
Sapendo che sin(π+α) = - sin(α) e cos(π+α) = - cos(α)
$$ \cot ( \pi + \alpha ) = \frac{ \cos (\pi + \alpha) }{ \sin (\pi + \alpha) } = \frac{ - \cos \alpha }{ - \sin \alpha } = \cot \alpha $$
Pertanto, la cotangente dell'angolo π+α è uguale alla cotangente di α.
In conclusione, gli angoli associati α e π+α hanno gli stessi valori della tangente e della cotangente.
Un esempio pratico
Devo calcolare il seno di 210°
$$ \sin 210° $$
Riscrivo i gradi come somma di 180° + 30°
$$ \sin 210° = \sin (180° + 30°) $$
che in radianti diventa
$$ \sin 210° = \sin ( \pi + \frac{\pi}{6} ) $$
Gli angoli π+α e α sono angoli associati dove α=π/6 (ossia 30°)
$$ \sin( \pi + \alpha ) = - \sin(\alpha) $$
Quindi, il seno di 210° è uguale al valore opposto del seno di 30°
$$ \sin 210° = \sin( \pi + \frac{\pi}{6} ) = - \sin( \frac{\pi}{6} ) $$
Sapendo che il seno di 30° è 1/2, il seno di 210° è -1/2.
$$ \sin 210° = \sin( \pi + \frac{\pi}{6} ) = - \sin( \frac{\pi}{6} ) = - \frac{1}{2} $$
$$ \sin 210° = - \frac{1}{2} $$
E così via.
