La seconda relazione fondamentale della trigonometria

La tangente di un angolo è uguale al rapporto tra il seno e il coseno dello stesso angolo. $$ \tan \alpha = \frac{ \sin \alpha }{ \cos \alpha } $$

Dimostrazione

Prendo in considerazione un angolo alfa nella circonferenza goniometrica

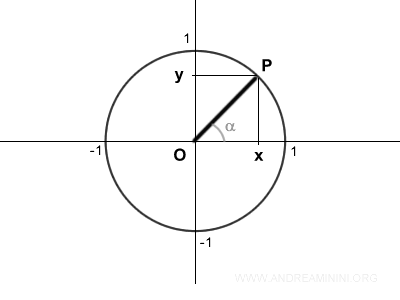
Il segmento OP è un tratto della retta r.

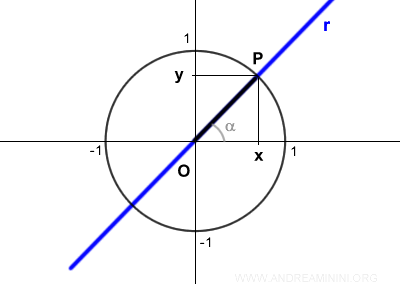
L'equazione di una retta passante per l'origine è y=mx dove m è il coefficiente angolare che determina l'inclinazione della retta.

$$ y = m \cdot x $$

Moltiplico entrambi i membri dell'equazione per 1/x per mettere in evidenza il coefficiente angolare.

$$ y \cdot \frac{1}{x} = m \cdot x \cdot \frac{1}{x} $$

e semplifico

$$ \frac{y}{x} = m $$

Quindi, la retta r ha un coefficiente angolare (m) pari al rapporto y/x.

$$ m = \frac{y}{x} $$

Sapendo che il coefficiente angolare della retta è uguale alla tangente dell'angolo alfa (vedi spiegazione).

$$ m = \frac{y}{x} = \tan \alpha $$

Poiché in una circonferenza goniometrica y=sin α e x=cos α

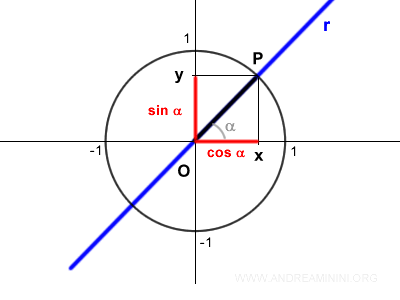
Quindi posso scrivere

$$ m = \frac{y}{x} = \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

In questo modo ho dimostrato la seconda relazione fondamentale della trigonometria

$$ \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

E così via.