Angoli associati alfa e meno alfa

In trigonometria gli angoli associati alfa (α) e meno alfa (-α) mi permettono di usare le seguenti formule di trasformazione. $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$

Essendo angoli associati gli angoli α e -α hanno lo stesso valore assoluto delle funzioni trigonometriche, seno, coseno, tangente e cotangente.

Dimostrazione e spiegazione

Considero un angolo α e l'angolo -α su una circonferenza goniometrica.

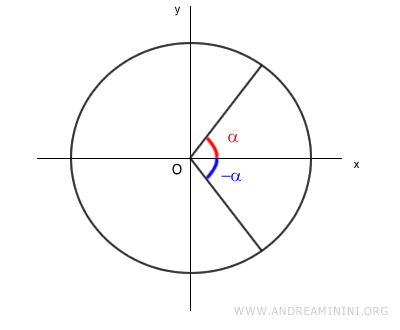
Gli angoli α e -α sono due angoli opposti.

Poi analizzo i valori delle funzioni goniometriche in questi angoli.

Seno

I due angoli opposti α e -α determinano due valori opposti del seno sull'asse delle ordinate sin(α) e sin(-α).

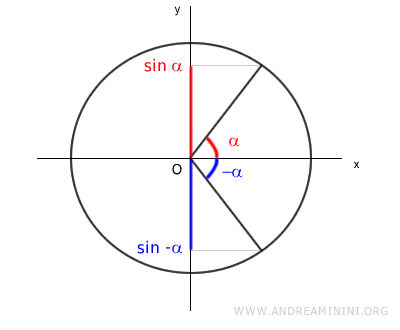
Essendo i due angoli α e -α degli angoli associati, i due valori del seno sono uguali in valore assoluto.

$$ \sin \alpha = | \sin - \alpha |$$

Poiché la funzione seno è una funzione dispari f(-x)=-f(x) posso scrivere sin(-α) come -sin(α).

$$ \sin - \alpha = - \sin \alpha $$

Le due forme sono equivalenti.

Coseno

Gli angoli opposti α e -α determinano lo stesso valore del coseno cos(α) e cos(-α) sull'asse delle ascisse.

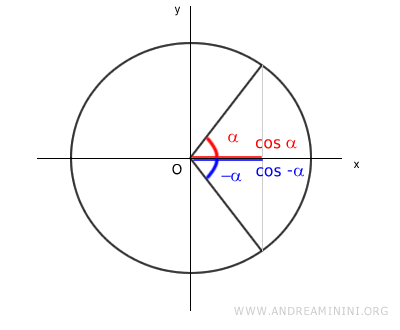
Ovviamente i due valori del coseno sono uguali anche in valore assoluto.

$$ \cos \alpha = | \cos - \alpha |$$

La funzione coseno è una funzione pari f(-x)=f(x) quindi posso scrivere cos(-α) anche come cos(α).

$$ \cos - \alpha = \cos \alpha $$

Le due forme sono equivalenti.

Una volta note le equivalenze del seno e del coseno degli angoli α e -α, posso calcolare quelle della tangente e della cotangente.

Tangente

La tangente di un angolo è pari al rapporto tra seno e coseno.

$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$

Nel caso dell'angolo -α la tangente è

$$ \tan -\alpha = \frac{\sin -\alpha}{\cos -\alpha} $$

Sapendo che sin -α = -sin α e cos -α = cos α posso scrivere

$$ \tan -\alpha = \frac{\sin -\alpha}{\cos -\alpha} = \frac{ - \sin \alpha}{ \cos \alpha} $$

Ne consegue che la tangente dell'angolo -α è uguale a meno tangente dell'angolo α

$$ \tan -\alpha = \frac{\sin -\alpha}{\cos -\alpha} = \frac{ - \sin \alpha}{ \cos \alpha} = - \tan \alpha $$

A questo punto dimostrare l'equivalenza tra la cotangente di α e -α come inversa della tangente.

Cotangente

La cotangente di un angolo è il rapporto tra il coseno e il seno dell'angolo.

$$ \cot \alpha = \frac{\cos \alpha}{\sin \alpha} $$

Nel caso dell'angolo -α la cotangente è

$$ \cot -\alpha = \frac{\cot -\alpha}{\sin -\alpha} $$

Sapendo che sin -α = -sin α e cos -α = cos α posso scrivere

$$ \cot -\alpha = \frac{\cot -\alpha}{\sin -\alpha} = \frac{ \cos \alpha}{ - \sin \alpha} $$

Pertanto, la cotangente dell'angolo -α è uguale a meno cotangente dell'angolo α.

$$ \cot -\alpha = \frac{\cot -\alpha}{\sin -\alpha} = \frac{ \cos \alpha}{ - \sin \alpha} = - \cot \alpha $$

Tutte le formule di trasformazione degli angoli α e -α sono dimostrate.

Un esempio pratico

Devo calcolare il seno di -30°

$$ \sin -30° $$

che in radianti diventa

$$ \sin - 30° = \sin ( - \frac{\pi}{6} ) $$

Sapendo che gli angoli opposti α=π/6 e -α=-π/6 sono angoli associati

$$ \sin( \alpha ) = - \sin(\alpha) $$

Quindi, il seno di -30° è uguale al valore opposto del seno di 30°

$$ \sin -30° = \sin ( - \frac{\pi}{6} )= - \sin( \frac{\pi}{6} ) $$

Sapendo che il seno di 30° è 1/2, il seno di -30° è -1/2.

$$ \sin -30° = \sin ( - \frac{\pi}{6} )= - \sin( \frac{\pi}{6} ) = - \frac{1}{2} $$

$$ \sin -30° = - \frac{1}{2} $$

E così via.