Arcocotangente
L'arcocotangente è la funzione trigonometrica inversa della cotangente. $$ y = arccotg \ x $$ Si idica con il simbolo arccotg, arccot, cotan-1 o cotg-1.
Dal punto di vista geometrico l'arcocotangente misura la lunghezza dell'arco in radianti sulla circonferenza goniometrica ossia l'angolo che determina il valore della cotangente.
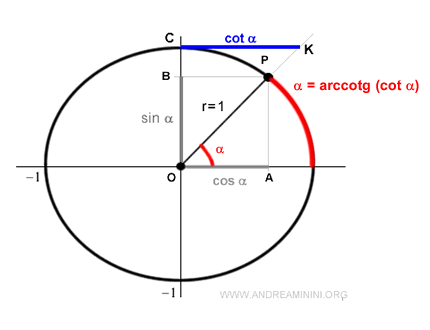
Ad esempio, la cotangente di un angolo di π/2 (90°) è zero.
$$ cotg \ \frac{\pi}{2} = 0 $$
Pertanto, l'arcocotangente di zero è π/2.
$$ arccotg \ 0 = \frac{\pi}{2} $$
Nota. Essendo una funzione inversa, l'arcocotangente di una cotangente è l'angolo della cotangente. $$ arccotg ( cotg \ \alpha ) = \alpha $$
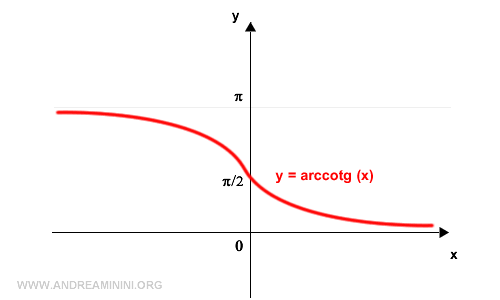
Il grafico della funzione arcocotangente
Il grafico della funzione arcocotangente è una funzione limitata entro l'estremo superiore π e l'estremo inferiore 0 ed è strettamente decrescente.
Come si costruisce il grafico dell'arcocotangente
La funzione cotangente è una funzione periodica.
Pertanto, è una funzione non invertibile sul proprio dominio perché non è biettiva.
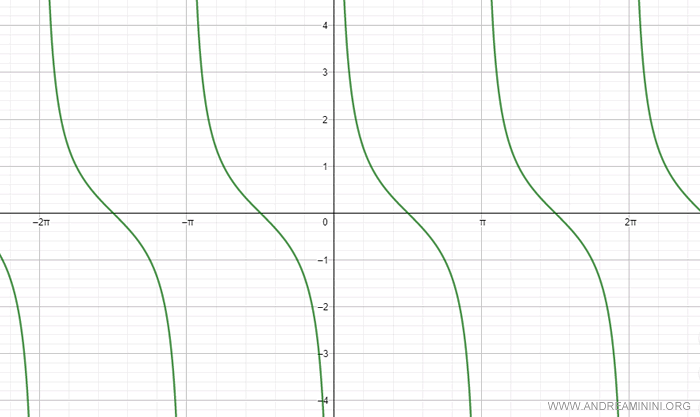
Tuttavia, se riduco il dominio all'intervallo di tempo (0,π) la funzione cotangente diventa biettiva (biunivoca).
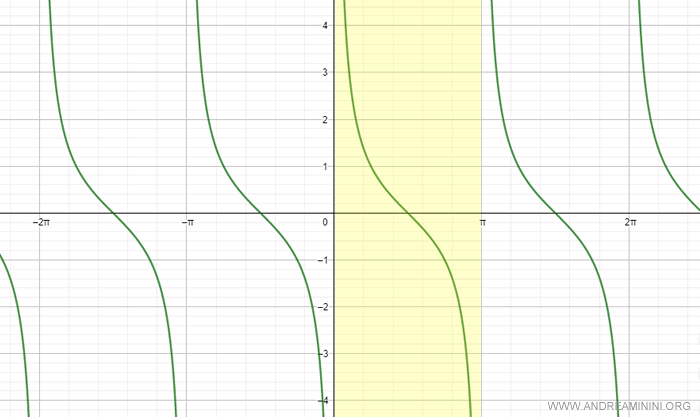
Nota. La funzione cotangente è biettiva anche in altri intervalli. Ad esempio (-π,0). Avrei potuto prendere anche altri intervalli per calcolare la funzione inversa.
Essendo biettiva nell'intervallo (0,π) la cotangente è anche una funzione invertibile in questo intervallo.
La funzione inversa della cotangente nell'intervallo (0,π) è l'arcocotangente.
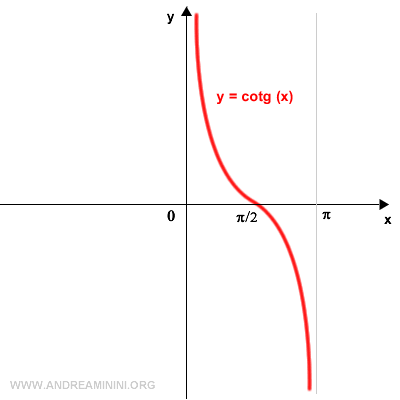
Per ottenere il grafico dell'arcocotangente ruoto il grafico della cotangente di 90° in senso antiorario.
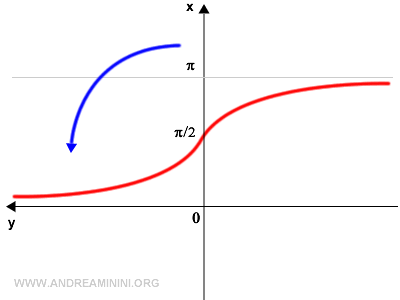
Poi rifletto il grafico in orizzontale rispetto all'asse verticale (x).
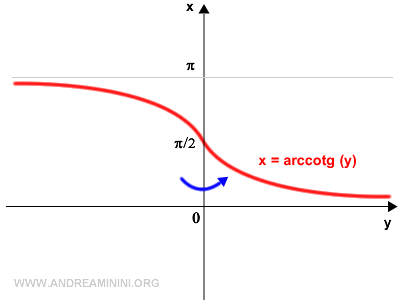
In questo modo ottengo il grafico dell'arcocotangente.
E così via
