La funzione arcocoseno
Cos'è l'arcocoseno
L'arcocoseno è la funzione goniometrica inversa del coseno nell'intervallo [0,π]. $$ arccos $$ Si indica con il simbolo arccos.
A volte l'arcocoseno è indicato anche il simbolo cos-1 dove il -1 non è un esponente ma il simbolo matematico della funzione inversa.
Come funziona l'arcocoseno
A partire dal valore y del coseno, l'arcocoseno calcola l'angolo x in radianti che lo determina.
Esempio
Il coseno della funzione vale 0.5
$$ cos \ \alpha \ = 0.5 $$
Quale angolo α determina questo valore del coseno?
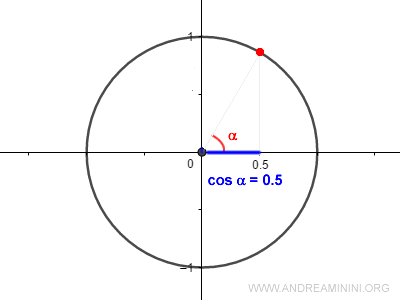
Per saperlo calcolo l'arcocoseno del coseno.
$$ \alpha = arccos (0.5) = \frac{ \pi }{ 3 } \ rad $$
L'arcocoseno individua la lunghezza x dell'arco sulla circonferenza determinato dal coseno.
L'arco è misurato in radianti e ha la stessa ampiezza dell'angolo x che determina il coseno.
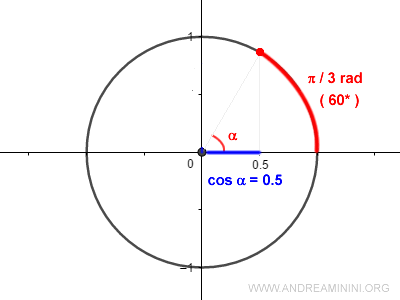
In questo esempio, la funzione cos α è uguale a 0.5 quando l'angolo x è uguale a π/3 radianti (60°).
La dimostrazione
La funzione coseno assume valori compresi tra -1 e +1.
Essendo una funzione periodica, lo stesso valore di cos(x) può essere ottenuto da diversi valori di x, ossia da diversi angoli. Ad esempio x1 e x2.
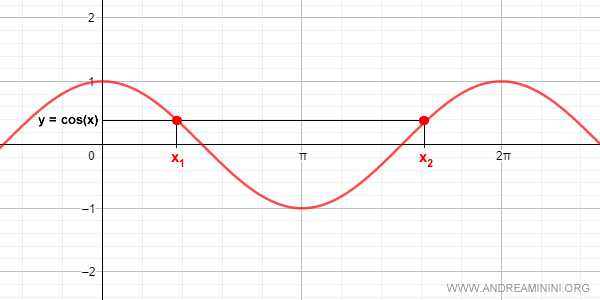
E' quindi impossibile costruire una funzione inversa del coseno su tutto il dominio di x perché si viola il principio dell'unicità del valore x rispetto a y=f(x).
$$ f:x -> y $$
Come si costruisce la funzione inversa del coseno?
A questo problema c'è una soluzione.
Prendendo in considerazione soltanto una parte del dominio della funzione coseno è possibile soddisfare l'unicità della x.
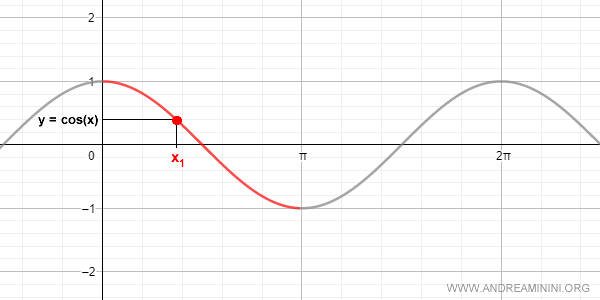
Nell'intervallo [0,π] di x si verifica una corrispondenza biunivoca tra il valore del coseno [-1,+1] e il valore della variabile x.
Pertanto, in questo intervallo posso costruire la funzione inversa del coseno.
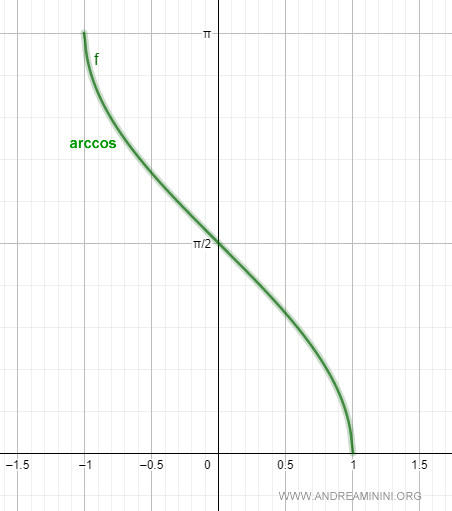
Questa funzione è detta arcocoseno.
$$ arccos(x) : [-1,1] → [0,π] $$
L'arcocoseno è indicato con la notazione arccos o acos.
A partire dal valore del coseno, la funzione arcocoseno calcola l'angolo x che lo determina nell'intervallo [0,π].
Nota. L'intervallo [0,π] non è l'unico in cui la funzione seno diventa invertibile. Ad esempio, posso invertire la funzione seno anche nell'intervallo [π,2π] e in infiniti altri intervalli in cui la funzione coseno diventa biettiva.
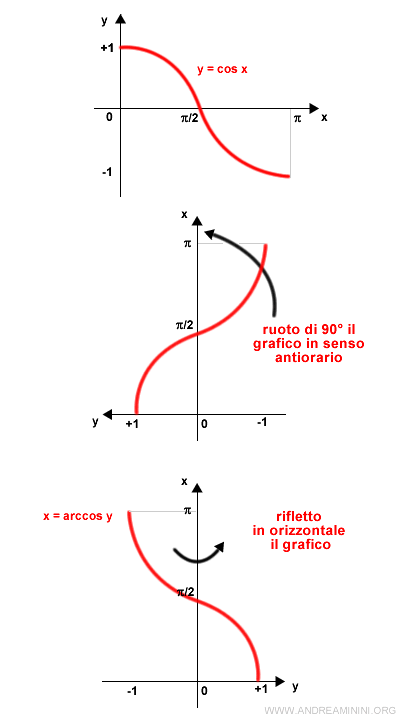
Come costruire il grafico della funzione arcocoseno
Posso ottenere il grafico dell'arcocoseno a partire dal grafico del seno nel dominio ridotto [0,π] tramite due passaggi:
- ruoto di 90° il grafico del coseno in senso antiorario
- rifletto in orizzontale il grafico
Il risultato finale è il grafico dell'arcocoseno.
Seguendo la stessa logica posso ottenere il grafico dell'arcocoseno partendo da altri domini ridotti.
Ad esempio, [-π,0] o altri intervalli in cui il seno è una funzione invertibile.
E così via.
