Teorema dei seni
I lati del triangolo sono proporzionali ai seni degli angoli opposti. $$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
Dove α, β, γ sono rispettivamente gli angoli opposti dei lati BC, AC, AB del triangolo.
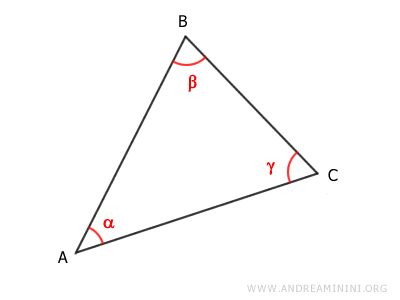
Questo teorema è anche conosciuto come teorema dei seni di Eulero.
Un esempio pratico
Devo risolvere un triangolo
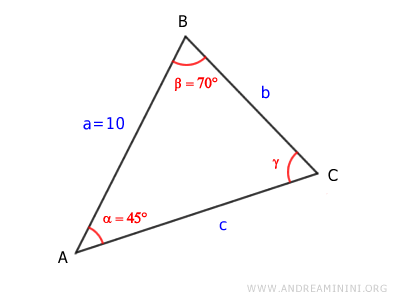
di cui conosco due angoli e la lunghezza di un lato
$$ \alpha = 45° $$
$$ \beta = 70° $$
$$ \overline{AB} = 10 $$
Per prima cosa calcolo l'angolo mancante.
Sapendo che in un triangolo la somma degli angoli è uguale a 180°, calcolo l'alngolo gamma per differenza.
$$ \alpha + \beta + \gamma = 180° $$
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma = 180° - 45° - 70° $$
$$ \gamma = 65° $$
Ora conosco tutti gli angoli del triangolo
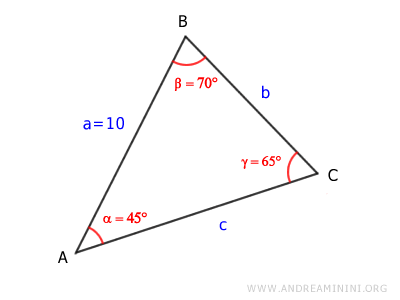
Una volta noti gli angoli, applico il teorema dei seni per calcolare la lunghezza dei lati.
$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
$$ \frac{\overline{AB}}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
Conosco già la lunghezza del lato AB ossia a=10
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
Ora confronto il primo membro dell'uguaglianza con il secondo per calcolare la lunghezza del segmento BC
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} $$
$$ \overline{BC} = \frac{10}{\sin 65°} \cdot \sin 45° $$
$$ \overline{BC} = 7,8 $$
Poi confronto il primo membro dell'uguaglianza con il terzo per misurare la lunghezza del segmento AC.
$$ \frac{10}{\sin 65°} = \frac{\overline{AC}}{\sin 70°} $$
$$ \overline{AC} = \frac{10}{\sin 65°} \cdot \sin 70° $$
$$ \overline{AC} =10,37 $$
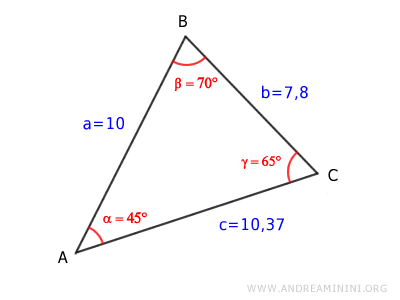
Pertanto, i lati del triangolo sono lunghi
$$ \overline{AB} = 10 $$
$$ \overline{BC} = 7,8 $$
$$ \overline{AC} = 10,37 $$
Ho così risolto il triangolo.
La dimostrazione
Prendo in considerazione un triangolo qualsiasi inscritto in una circonferenza di raggio r.
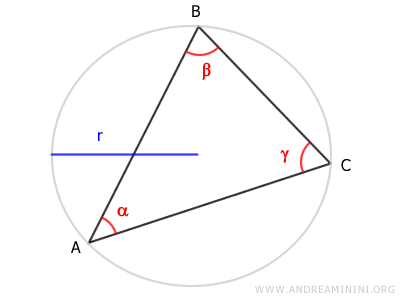
Secondo il teorema della corda, ogni lato del triangolo è pari al prodotto tra il diametro della circonferenza (2r) e il seno dell'angolo opposto.
$$ \overline{AB} = 2r \cdot \sin \gamma $$
$$ \overline{AC} = 2r \cdot \sin \beta $$
$$ \overline{BC} = 2r \cdot \sin \alpha $$
Metto in evidenza il diametro (2r) in ogni relazione
$$ \frac{ \overline{AB} }{ \sin \gamma } = 2r $$
$$ \frac{ \overline{AC} }{ \sin \beta } = 2r $$
$$ \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
Ogni rapporto è uguale al diametro 2r.
Pertanto vale la seguente relazione di uguaglianza
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
Questo vuol dire che i lati del triangolo sono proporzionali ai seni degli angoli opposti
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } $$
Ho dimostrato il teorema dei seni.
E così via.
