Metodo per memorizzare il seno, coseno e tangente per gli angoli di 0°, 30°, 45°, 60° e 90°
Questo metodo usa le dita di una mano per ricordare i valori del seno, coseno e tangente degli angoli 0°, 30°, 45°, 60° e 90°.
Si basa sul numero di dita alla sinistra e alla destra di un dito che rappresenta un angolo specifico.
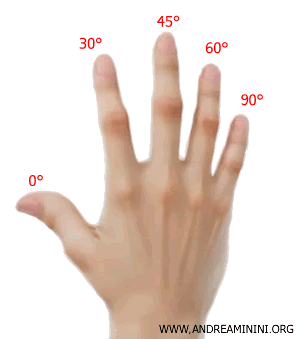
A ciascun dito della mano destra è assegnato un angolo $ \alpha $
- Pollice: 0°
- Indice: 30°
- Medio: 45°
- Anulare: 60°
- Mignolo: 90°
A questo punto per calcolare il coseno, il seno e la tangente di un angolo $ \alpha $, guardo il dito associato all'angolo $ \alpha $ e utilizzo queste formule:
- Coseno dell'angolo
Il coseno di un angolo $ \alpha $ è dato dalla radice quadrata del numero di dita a destra del dito che rappresenta l'angolo, diviso 2. $$ \cos( \alpha ) = \frac{ \sqrt{ \text{numero delle dita a destra} } }{2} $$ - Seno dell'angolo
Il seno di un angolo è dato dalla radice quadrata del numero di dita a sinistra del dito che rappresenta l'angolo, diviso 2. $$ \sin( \alpha ) = \frac{ \sqrt{ \text{numero delle dita a sinistra} } }{2} $$ - Tangente dell'angolo
La tangente dell'angolo $ \alpha $ è semplicemente il seno diviso per il coseno. $$ \tan{\alpha} = \frac{ \sin{ \alpha } }{ \cos{ \alpha }} $$
Questo metodo mi permette di trovare rapidamente i valori trigonometrici di questi angoli usando solo le dita di una mano.
Nota. Per usare la mano sinistra anziché la destra, basta invertire le due formule del seno e del coseno. Ho preferito usare la mano destra perché è più facile da ricordare.
Un esempio pratico
Devo calcolare il coseno, il seno e la tangente di 60°
L'angolo di 60° è associato al dito anulare della mano destra.
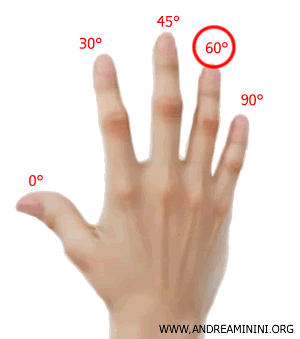
A destra del dito anulare c'è solo un dito (1), il migliolo, quindi il coseno di 60° è:
$$ \cos( 60° ) = \frac{ \sqrt{ \text{num. dita a destra} } }{2} = \frac{ \sqrt{1} }{2} = \frac{1}{2} $$
A sinistra del dito anulare ci sono 3 dita, quindi il seno di 60° è
$$ \sin( 60° ) = \frac{ \sqrt{ \text{num. dita a sinistra} } }{2} = \frac{ \sqrt{3} }{2} $$
Infine, una volta noti i valori del seno e del coseno, posso calcolare anche il valore della tangente di 60° tramite il rapporto $ tan(a)=sin(a)/cos(a) $.
$$ \tan(60°) = \frac{\sin(60°)}{\cos(60°)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} $$
Tutti i valori sono corretti.
| Angolo | Seno | Coseno | Tangente | |
|---|---|---|---|---|
| Radianti | Gradi | |||
| 0 | 0° | 0 | 1 | 0 |
| π/6 | 30° | 1/2 | √3/2 | √3/3 |
| π/4 | 45° | √2/2 | √2/2 | 1 |
| π/3 | 60° | √3/2 | 1/2 | √3 |
| π/2 | 90° | 1 | 0 | ∞ |
E così via.
