Cotangente
Nella circonferenza goniometrica la cotangente di un angolo alfa è l'inverso della tangente ed è pari al rapporto tra il coseno e il seno dell'angolo alfa. $$ \cot \ \alpha = \frac{1}{\tan \alpha} = \frac{\cos \alpha}{\sin \alpha} $$ Si indica con il simbolo cot oppure ctg, cotg.
Dal punto di vista geometrico la cotangente corrisponde al segmento CK.
Si ottiene prolungando il raggio OP fino all'intersezione K con una retta parallela all'ascisse e tangente alla circonferenza goniometrica CK.
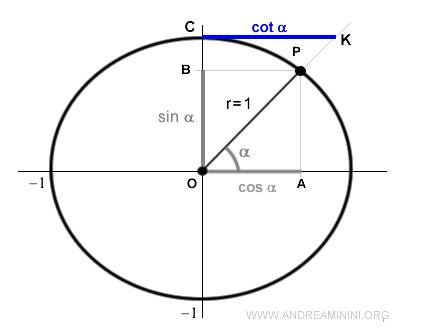
Per definizione la cotangente è il rapporto tra l'ascissa OA e l'ordinata OB di un punto P.
Da questa definizione derivano le altre formule.
$$ cotg \ \alpha = \frac{\overline{OA}}{\overline{OB}} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$
Dove il segmento OA è il coseno e il segmento OB è il seno dell'angolo α che individua il punto P.
Nota. La cotangente non è definita negli angoli in cui l'ordinata è nulla. In questi punti si verifica una divisione per zero e il rapporto non è definito perché le ordinate si trovano al denominatore. Pertanto, la cotangente non è definita negli angoli in cui il seno è nullo.
Il termine "cotangente" venne usato per la prima volta dal matematico inglese Edmund Gunter nel XVII secolo.
Le caratteristiche della funzione cotangente
La cotangente una funzione periodica che si ripete dopo ogni periodo π (ossia 180°).
$$ cotg \ \alpha = \cot( \alpha + n \cdot \pi ) $$
Ecco il grafico della cotangente da -2π a 2π.
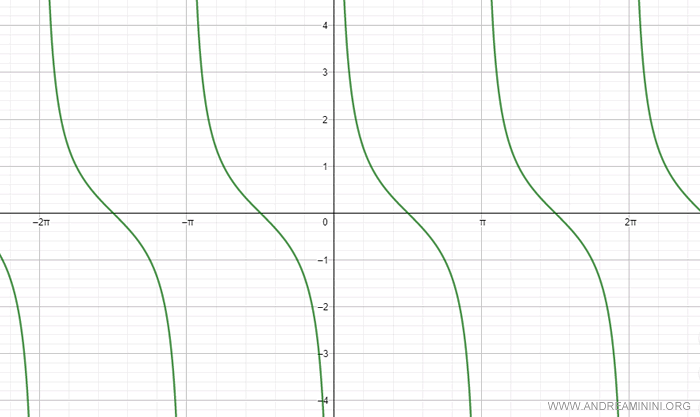
Nota. Essendo una funzione periodica con periodo π può essere studiata nell'intervallo (0, π). In quest'intervallo del dominio la cotangente è una funzione continua, monotòna, decrescente.
La cotangente non è definita nell'angolo 0 e in ogni angolo periodico k·π dove k è un numero intero, quando il seno al denominatore è nullo (sen 0=0).
$$ \alpha = k \cdot \pi $$
Nel grafico della cotangente si presentano degli asintoti verticali negli angoli α=k·n dove la cotangente non è definita.
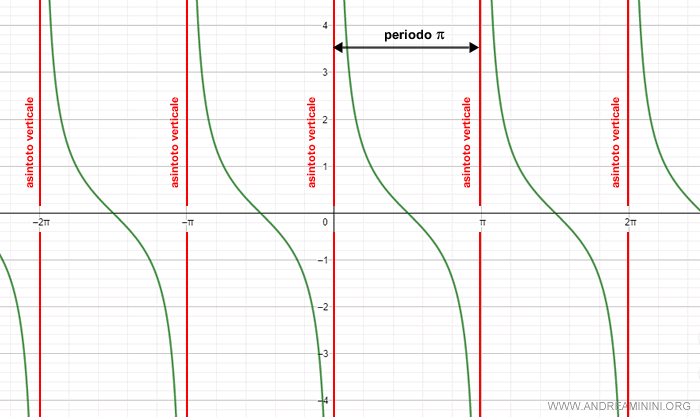
Il dominio della funzione cotangente è l'insieme dei numeri reali ridotto dei multipli interi di π.
$$ cotg \ \alpha : \ R \ - \ k \cdot \pi \ \ \rightarrow R \ \ \ \ con \ k \in Z $$
Il codominio è, invece, l'insieme dei numeri reali.
Pertanto il valore della cotangente varia da -∞ a +∞.
Gli angoli particolari della cotangente
In questa tabella sono descritti i principali angoli della cotangente.
| gradi | radianti | cotangente |
|---|---|---|
| 0° | 0 | non esiste |
| 15° | π/12 | 2+√3 |
| 30° | π/6 | √3 |
| 45° | π/4 | 1 |
| 60° | π/3 | (√3)/3 |
| 75° | 5π/12 | 2-√3 |
| 90° | π/2 | 0 |
| 180° | 0 | non esiste |
| 270° | 3π/2 | 0 |
| 360° | 0 | non esiste |
La dimostrazione
Prendo in considerazione un angolo α che individua un punto P sulla circonferenza goniometrica.
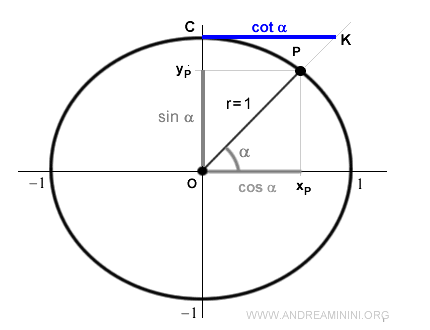
La cotangente è la funzione che associa all'angolo α il rapporto tra l'ascissa xP e l'ordinta yP del punto P.
$$ cotg \ \alpha = \frac{x_P}{y_P} $$
In una circonferenza goniometrica l'ascissa xP è il coseno mentre l'ordinata yP è il seno.
$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} $$
Sapendo che la tangente è il rapporto tra seno e coseno tan=sin/cos, il reciproco della tangente è 1/tan=cos/sin.
Quindi posso scrivere la cotangente anche come reciproco della tangente.
$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$
Nota. L'uguaglianza tra la cotangente e il reciproco della tangente si verifica solo quando l'angolo alfa non è un multiplo di π e di π/2 $$ cotg \ \alpha = \frac{1}{\tan \alpha} \ \ \ , con \ \alpha \ne k \cdot \frac{\pi}{2} $$ perché nei multipli di π non è definita la cotangente mentre nei multipli di π/2 non è definita la tangente. Pertanto, l'uguaglianza tra cotangente e reciproco della tangente si verifica in un insieme più ristretto rispetto al dominio della cotangente.
Dimostrazione geometrica
Prendo un angolo orientato qualsiasi diverso da π e π/2.
Nella circonferenza goniometrica i triagoli sono simili perché hanno gli stessi angoli.
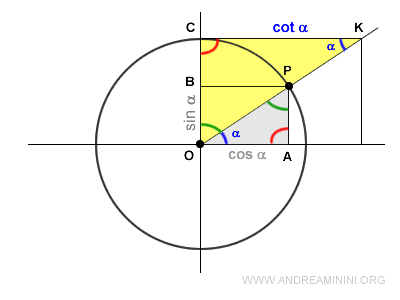
Essendo triangoli simili, c'è una proporzione fra i cateti corrispondendi
$$ \overline{CK} \ : \ \overline{OA} = \overline{OC} \ : \ \overline{AP} $$
ossia
$$ \frac{ \overline{CK} }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$
Sapendo che il segmento CK è la cotangente dell'angolo α.
$$ \frac{ cotg \ \alpha }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$
Il segmento OC è uguale al raggio della circonferenza goniometrica r=1.
$$ \frac{ cotg \ \alpha }{ \overline{OA} } = \frac{ 1 }{ \overline{AP} } $$
Il segmento OA è il coseno dell'angolo α mentre il segmento AP è il seno dell'angolo α.
$$ \frac{ cotg \ \alpha }{ \cos \alpha } = \frac{ 1 }{ \sin \alpha } $$
Metto in evidenza la cotangente e ottengo la formula che volevo dimostrare
$$ cotg \ \alpha = \frac{ \cos \alpha }{ \sin \alpha } $$
La funzione inversa della cotangente
La funzione inversa della cotangente è l'arcocotangente.
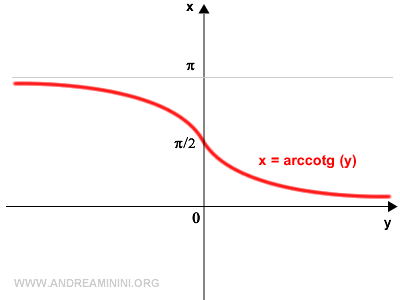
La cotangente non invertibile sul proprio dominio perché è una funzione periodica.
Tuttavia, se riduco il dominio della funzione all'intervallo di tempo (0,π) la funzione cotangente diventa biettiva.
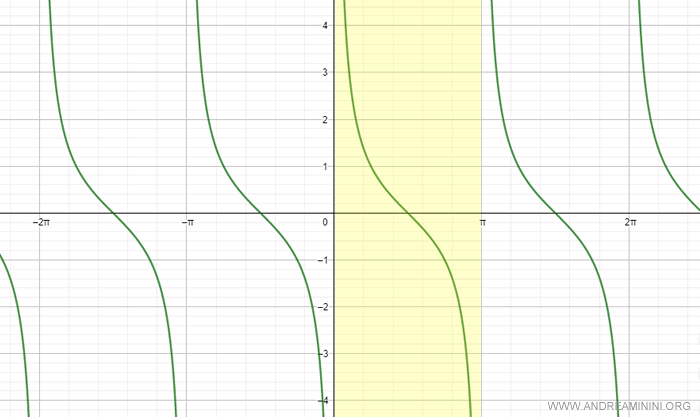
Nota. Esistono infiniti intervalli in cui la funzione cotangente è biettiva. Ad esempio (-π,0) o (π,2π) . Generalmente si utilizza l'intervallo (0,π). All'occorrenza posso partire anche da un intervallo diverso.
Nell'intervallo (0,π) la cotangente è una funzione invertibile.
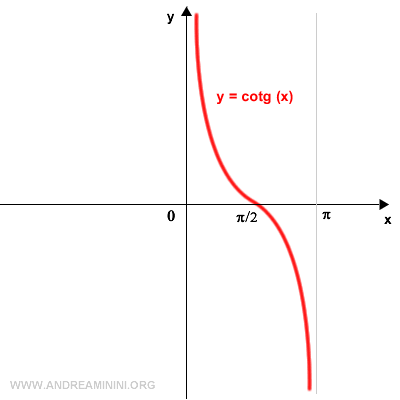
Per ottenere il grafico della funzione inversa effettuo una rotazione di 90° del grafico in senso antiorario.
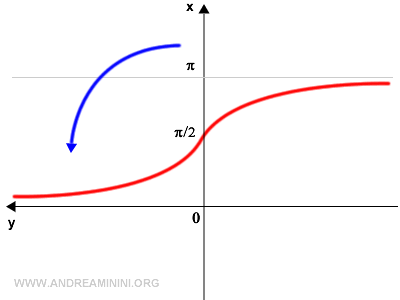
Poi ribalto il grafico in orizzontale con una riflessione rispetto all'asse verticale.
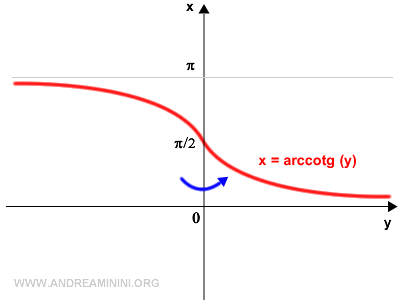
In questo modo ottengo il grafico della funzione inversa della cotangente ossia dell'arcocotangente.
E così via.
