Coseno iperbolico
Il coseno iperbolico (cosh) è una delle funzioni iperboliche della trigonometria. $$ \cosh(x) $$ Il dominio della funzione è l'insieme dei numeri reali (-∞;∞) mentre il codominio è l'intervallo [1;∞)
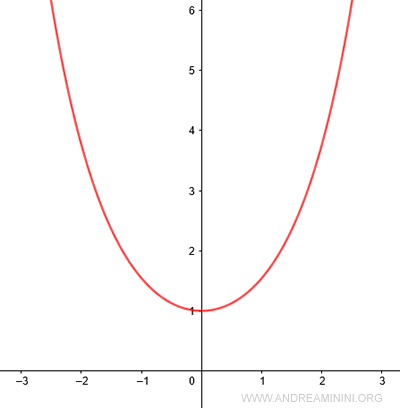
A differenza del coseno, il coseno iperbolico non viene calcolato sulla circonferenza goniometrica ma sull'iperbole equilatera x2-y2=1.
La spiegazione
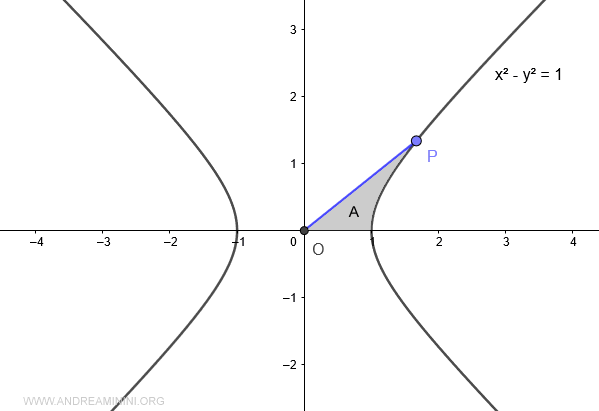
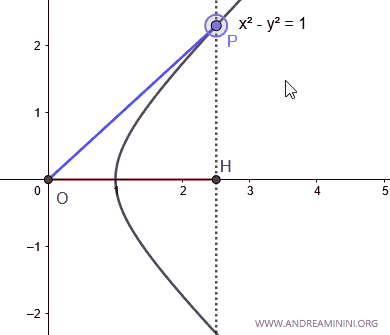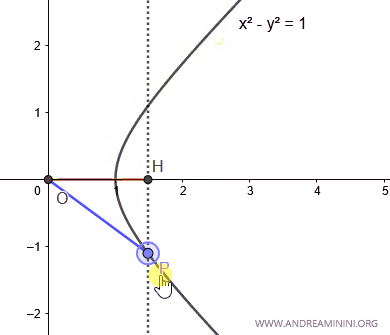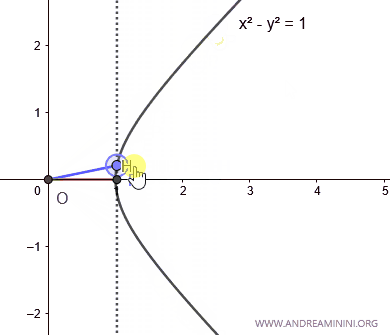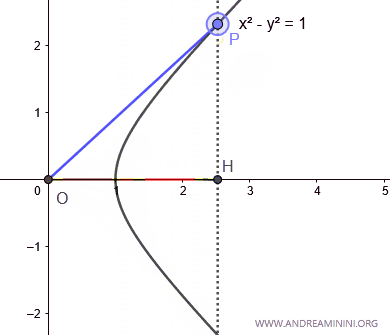
Traccio il grafico dell'iperbole equilatera x2-y2=1 sul diagramma cartesiano.
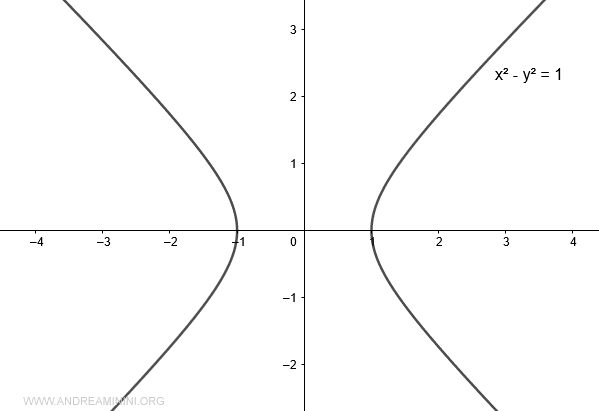
Considero solo l'iperbole nel I e nel IV quadrante.
Prendo un punto P sull'iperbole equilatera.
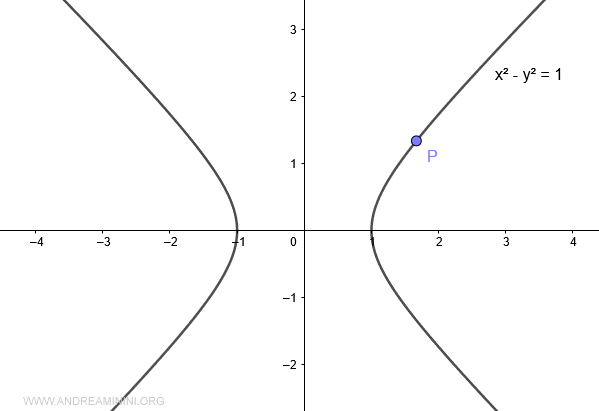
Poi congiungo il punto P con l'origine O del diagramma.
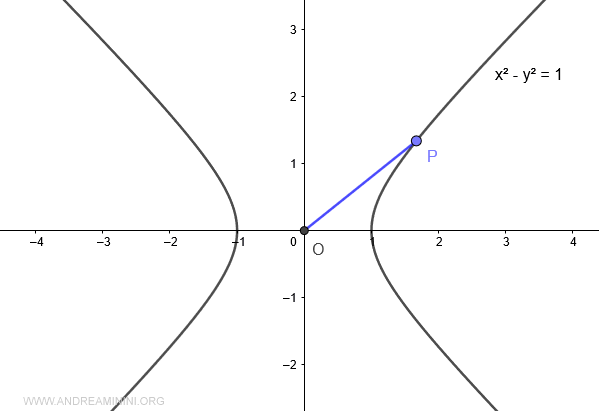
Il segmento OP ha un'apertura angolare delimitata tra (-π/4 ; π/4) ossia tra (-45°;45°)
L'area A che si forma tra l'asse delle ascisse, l'iperbole e il segmento OP è l'argomento (x) del coseno iperbolico cosh(x). E' setto settore iperbolico.
Nota. A differenza delle funzioni goniometriche (seno, coseno, tangente, ecc.) nelle funzioni iperboliche l'argomento non è un angolo.
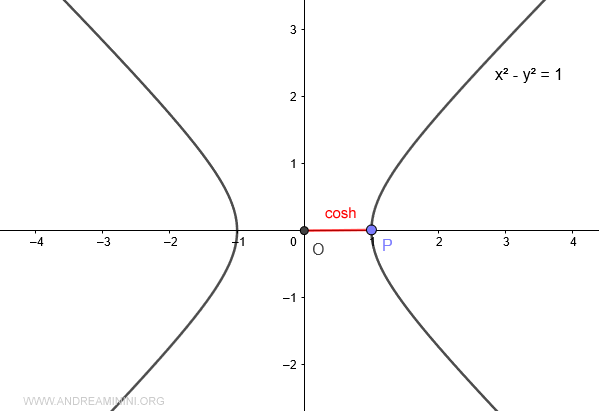
Il valore del coseno iperbolico cosh(x) è la proiezione del punto P sull'asse delle ascisse.
Pertanto, quando l'area A=0 è uguale a zero, il valore del coseno iperbolico è uguale a 1.
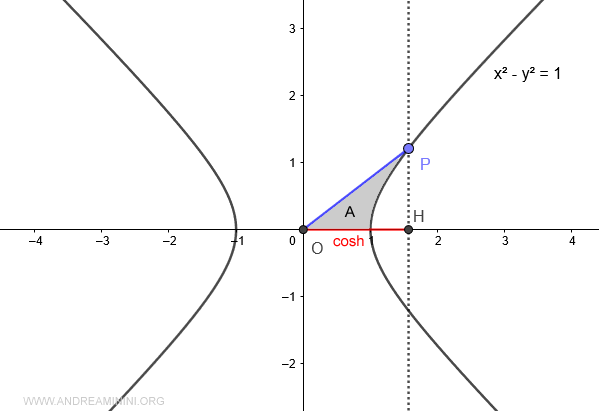
Quando l'area A>0 è maggiore di zero il coseno iperbolico è un numero positivo.
Quando l'area A<0 è minore di zero il coseno iperbolico è un numero negativo.
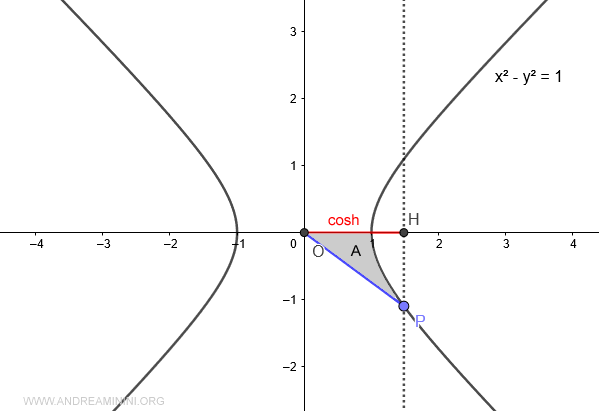
Nota. L'area del settore iperbolico è negativa quando il punto P ha un'ordinata negativa. Viceversa, è positivo se il punto P ha un'ordinata positiva.
L'area del settore iperbolico tende a crescere all'infinito quando l'ascissa del punto P tende a infinito.
Quindi, l'area del settore iperbolico è non limitato ed è un numero reale compreso nell'intervallo (-∞;∞).
Il valore del coseno iperbolico, invece, è sempre positivo ed è un numero reale compreso nell'intervallo [1;∞).
E così via.
