Secante
Cos'è la secante
In trigonometria la secante è una funzione che associa a un angolo α il reciproco del coseno. Si indica con sec. $$ \sec \alpha = \frac{1}{\cos \alpha} $$
Dal punto di vista geometrico, la secante (OB) è l'intersezione tra la retta (r) tangente a un punto P sulla circonferenza goniometrica e l'asse delle ascisse.
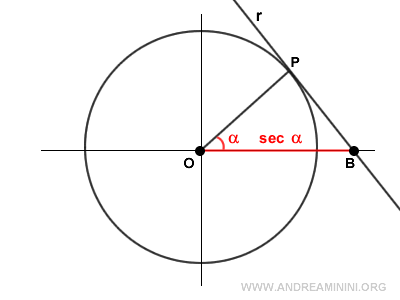
La secante è anche il segmento OC che esce dall'origine O, passa per il punto P e interseca la tangente nel punto C.
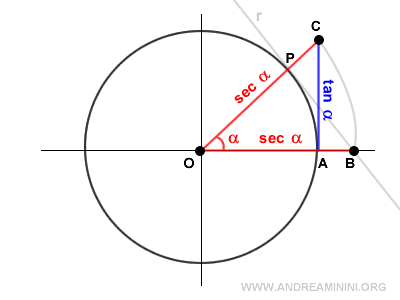
La funzione secante è definita nell'insieme dei numeri reali R tranne nei punti π/2+kπ con k intero, dove il coseno è nullo.
$$ \sec \alpha \ : \ R - \frac{\pi}{2}+k \cdot \pi \rightarrow R - (-1,1) \ \ \ \ \ \ \ \ k \in Z $$
Il codominio è l'insieme dei numeri reali R tranne l'intervallo (-1,1)
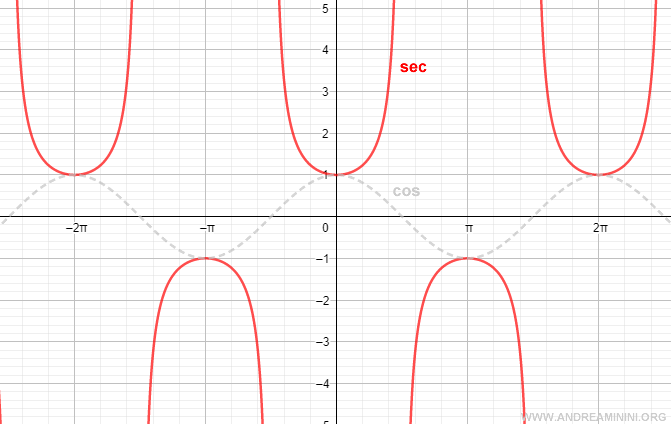
Dal punto di vista matematico la secante è una funzione pari perché f(x) = f(-x).
E' anche una funzione periodica e può essere studiata nell'intervallo (0,2π).
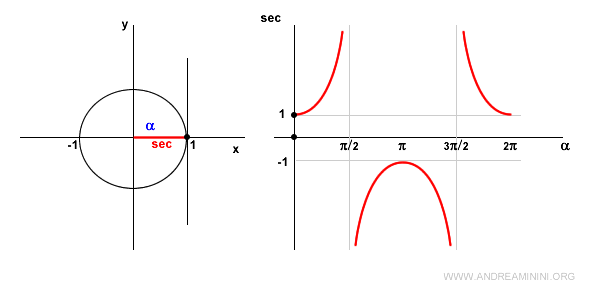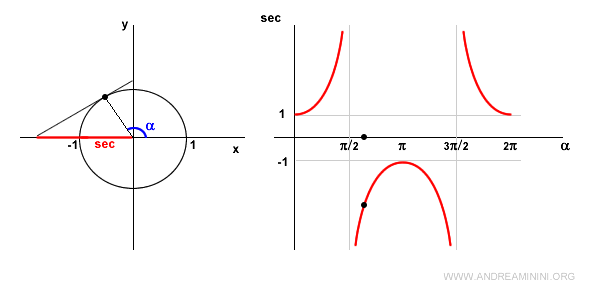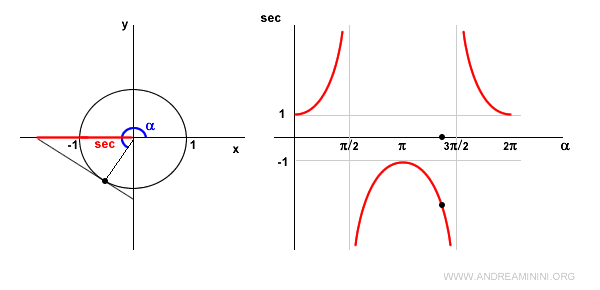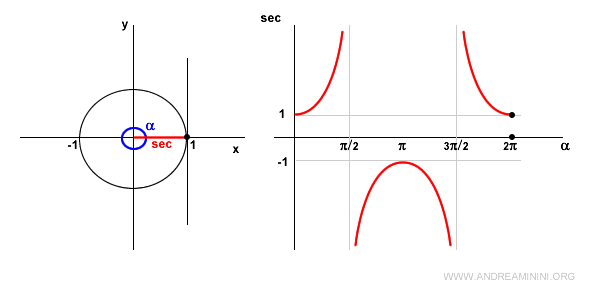
Nota. La funzione secante è indefinita nei punti π/2+kπ con k intero. In questi punti si presenta un asintoto verticale.
Ecco alcuni valori notevoli della secante che conviene tenere a mente.
| gradi | radianti | secante |
|---|---|---|
| 0° | 0 | 1 |
| 45° | π/4 | √2 |
| 60° | π/3 | 2 |
| 90° | π/2 | indefinita |
| 120° | 2π/3 | -2 |
| 180° | π | -1 |
| 270° | 3/2π | indefinita |
| 360° | 2π | 1 |
La dimostrazione
Il triangolo OAC è simile al triangolo ODP.
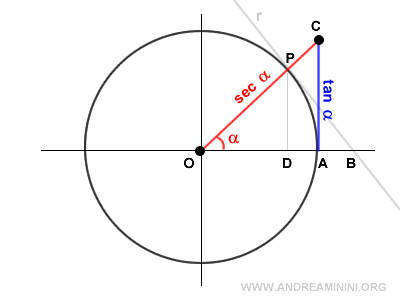
Quindi, posso scrivere la seguente proprozione
$$ \overline{OP} \ : \overline{OD} = \overline{OC} \ : \overline{OA} $$
ossia
$$ \frac{ \overline{OP} } { \overline{OD} } = \frac{ \overline{OC} } { \overline{OA} } $$
Il segmento OD è il coseno dell'angolo alfa
$$ \frac{ \overline{OP} } { \cos \alpha } = \frac{ \overline{OC} } { \overline{OA} } $$
Poiché il raggio della circonferenza goniometrica è uguale a uno, sostituisco OA=1 e OP=1
$$ \frac{ 1 } { \cos \alpha } = \frac{ \overline{OC} } { 1 } $$
$$ \frac{ 1 } { \cos \alpha } = \overline{OC} $$
Il segmento OC è la secante dell'angolo alfa
$$ \frac{ 1 } { \cos \alpha } = \sec \alpha $$
Ho così ottenuto la formula della secante come reciproco del coseno.
Dimostrazione alternativa. I triangoli OPB e OPD sono simili perché hanno gli angoli della stessa ampiezza.
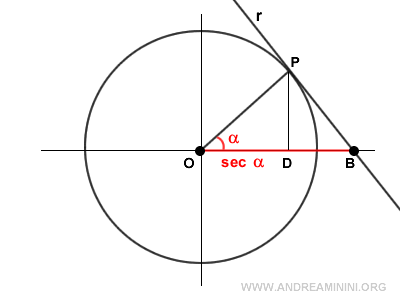
Pertanto, hanno la stessa proporzione tra il cateto e l'ipotenusa. $$ \frac{ \overline{OD} } { \overline{OP} } = \frac{ \overline{OP} } { \overline{OB} } $$ Sapendo che OB è la secante. $$ \frac{ \overline{OD} } { \overline{OP} } = \frac{ \overline{OP} } { \sec \alpha } $$ Il segmento OD è il coseno $$ \frac{ \cos \alpha } { \overline{OP} } = \frac{ \overline{OP} } { \sec \alpha } $$ ll segmento OP è il raggio unitario della circonferenza goniometrica, ossia OP=1. $$ \frac{ \cos \alpha } { 1 } = \frac{ 1 } { \sec \alpha } $$ Metto in evidenza la secante e ottengo la formula che volevo dimostrare. $$ \frac{ \sec \alpha } { 1 } = \frac{ 1 } { \cos \alpha } $$
Altre formule della secante
La secante dell'angolo α può essere calcolata anche a partire dalla tangente dell'angolo α. $$ \sec \alpha = \sqrt{1+ \tan^2 \alpha } $$ ovvero $$ \sec^2 \alpha = 1+ \tan^2 \alpha $$
Dimostrazione
Il raggio, la secante e la tangente formano un triangolo rettangolo, in cui la secante è l'ipotenusa.
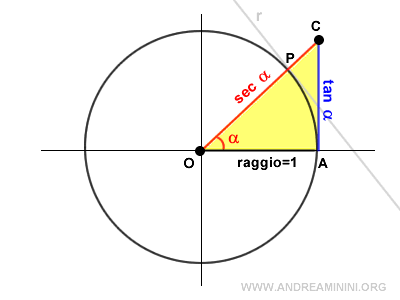
Quindi, posso ottenere la secante tramite il teorema di Pitagora in funzione della tangente.
$$ \sec \alpha = \sqrt{1^2+ \tan^2 \alpha } $$
$$ \sec \alpha = \sqrt{1+ \tan^2 \alpha } $$
Elevo al quadrato entrambi i lati dell'equazione
$$ ( \sec \alpha )^2 = ( \sqrt{1+ \tan^2 \alpha } )^2 $$
$$ \sec^2 \alpha = 1+ \tan^2 \alpha $$
Il grafico della secante
Quando l'angolo ha un ampiezza nulla α=0 la secante è uguale a 1, perché cos 0 = 1.
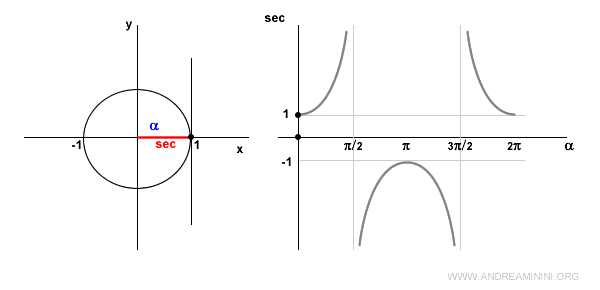
Quando l'angolo α si trova nel I quadrante il coseno è positivo, quindi anche la secante è positiva e crescente.
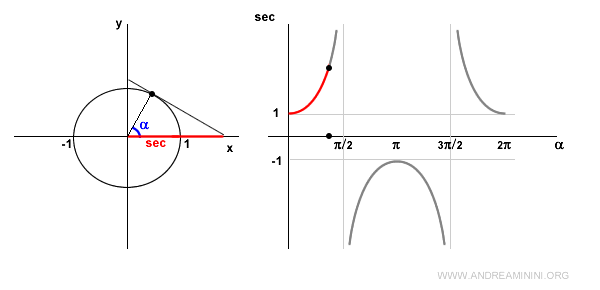
Quando l'angolo α=π/2 (90°) la secante non è definita perché cos π/2 = 0 e il rapporto sec π/2 = 1/0 non è definito.
In questo caso la retta tangente al punto è parallela all'asse delle ascisse. Pertanto non esiste un punto di intersezione tra le due rette.
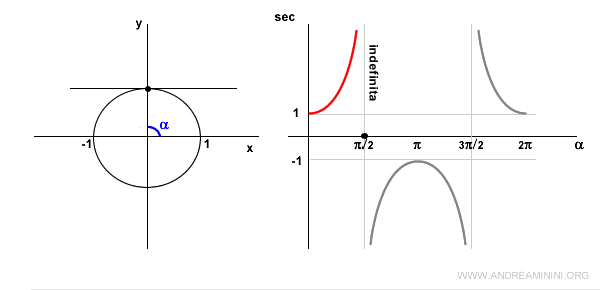
Quando l'angolo α si trova nel II quadrante il coseno è negativo, quindi anche la secante è negativa e crescente.
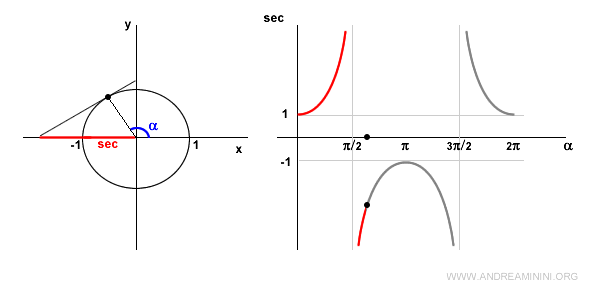
Quando l'angolo α=π (180°) il coseno è cos π = -1.
Quindi, la secante è sec π = -1.
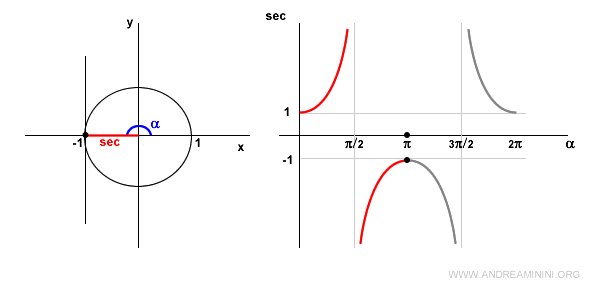
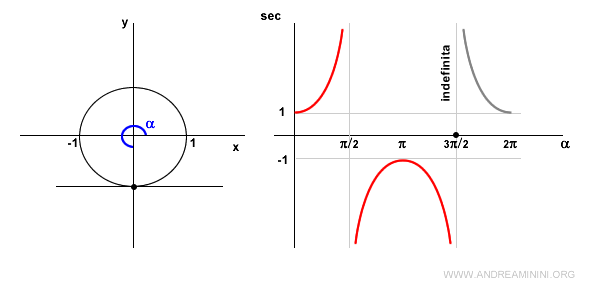
Quando l'angolo α si trova nel III quadrante il coseno è ancora negativo.
Quindi la secante è negativa ma decrescente.
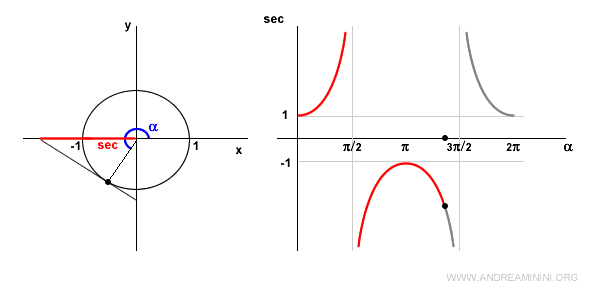
Quando l'angolo α=3π/2 (270°) il coseno è nullo. Quindi la secante non è definita perché il rapporto 1/0 non è definito.
Anche in questo caso la retta tangente è parallela all'asse delle ascisse, pertanto senza punti di intersezione.
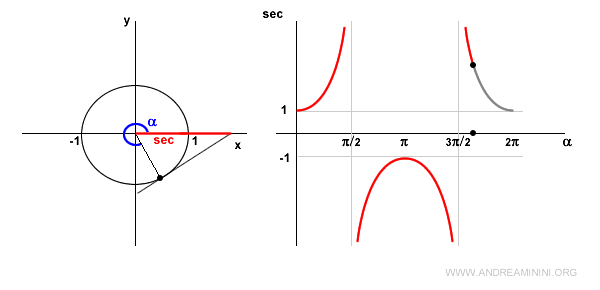
Quando l'angolo α si trova nel IV quadrante il coseno è positivo.
Quindi, anche la secante è positiva e decrescente.
In α=2π si torna alla stessa situazione di un angolo di ampiezza nulla α=0.
Quindi, la secante è pari a 1.
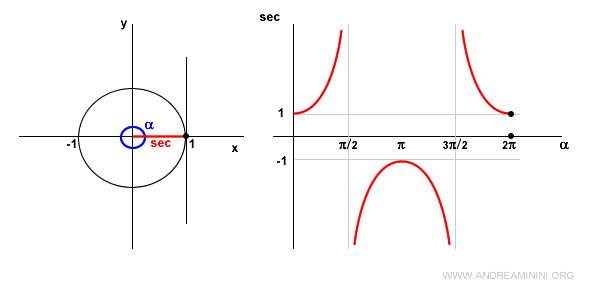
Essendo una funzione periodica, da questo punto in poi tutto si ripete da capo.
E così via.
