La circonferenza goniometrica
Cos'è la circonferenza goniometrica
La circonferenza goniometrica è una circonferenza con raggio unitario (r=1), un punto di origine degli archi (A) e un verso antiorario con segno positivo.
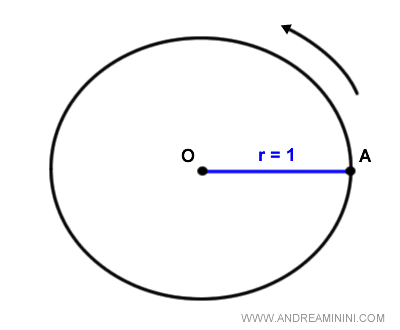
Dove il punto A si trova alle coordinate (x;y)=(1;0) ed è detto origine degli archi.
La circonferenza goniometrica è usata per misurare gli angoli.
Una volta preso un punto P qualsiasi della circonferenza, l'angolo è determinato dal vertice POA.
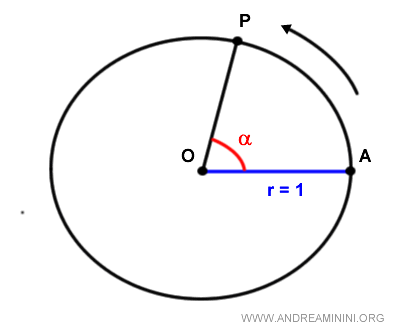
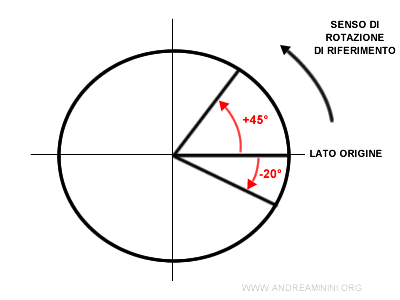
L'angolo è un angolo orientato poiché nella circonferenza goniometrica c'è un verso antiorario prefissato.
- L'angolo ha segno positivo se mi sposto sulla circonferenza in senso antiorario.
- L'angolo ha segno negativo se mi sposto sulla circonferenza in senso orario.
Nota. Il centro della circonferenza coincide con l'origine O degli assi cartesiani ossia con il punto alle coordinate (0,0) prendendo l'asse delle ascisse positivo (x) come lato origine degli angoli orientati. Quindi il punto A di origine degli archi si trova alle coordinate (1,0) del piano cartesiano.
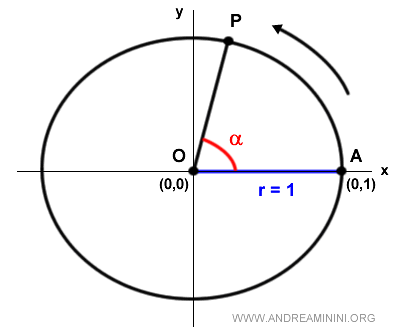
Poiché il raggio è unitario (r=1) l'equazione della circonferenza goniometrica sul piano cartesiano è $$ x^2+ y^2 = 1 $$
Come misurare l'ampiezza dell'angolo
L'ampiezza dell'angolo è misurato in radianti (rad) se non specificato diversamente.
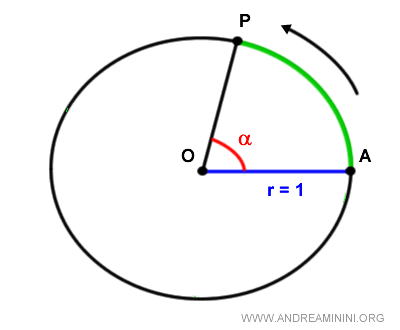
L'ampiezza dell'angolo in radianti è pari al rapporto fra l'arco AP sulla circonferenza goniometrica e il raggio OA.
$$ \alpha = \frac{\overline{AP}}{\overline{OA}} \ rad $$
Quindi, nella circonferenza goniometrica un radiante è un arco AP di lunghezza pari al raggio OA.
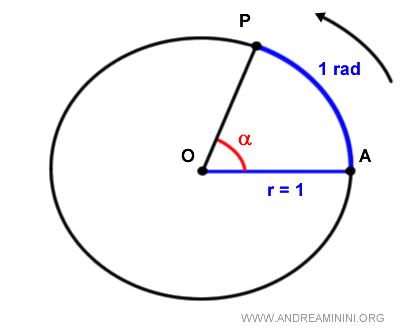
In questo caso specifico AP=OA e il rapporto è pari a 1
$$ se \ \overline{AP} = \overline{OA} \ \Rightarrow \ \frac{\overline{AP}}{\overline{OA}} = 1 \ rad $$
Il radiante (rad) è l'unità di misura universalmente riconosciuta dell'ampiezza dell'angolo.
Nota. Ci sono anche altre unità di misura per misurare l'angolo. Ad esempio, in gradi. Tuttavia, l'angolo deve essere misurato in gradi sessagesimali o decimali solo se espressamente specificato dal problema.
Perché misurare gli archi in radianti
La lunghezza di un arco di circonferenza in radianti si ottiene con la formula
$$ l = \alpha \cdot r $$
Dove l è la lunghezza dell'arco, alfa è l'angolo e r è il raggio.
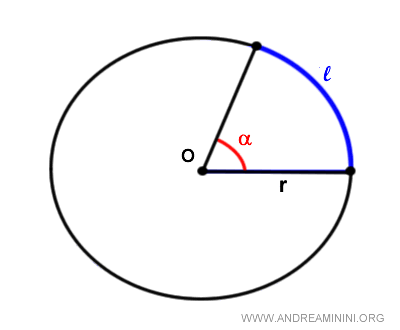
In una circonferenza goniometrica il raggio è uguale a uno (r=1).
$$ l = \alpha \cdot 1 $$
Quindi, nella circonferenza goniometrica la lunghezza dell'arco in radianti coincide con la misura dell'angolo.
$$ l = \alpha $$
E' uno dei vantaggi della misura degli angoli in radianti (rad).
E così via.
