L'arcotangente
Cos'è l'arcotangente
In trigonometria l'arcotangente è la funzione inversa della funzione tangente. Si indica con il simbolo arctg, arctan, tg-1 o tan-1. $$ y = arctan \ x $$
L'argomento x è il valore della tangente.
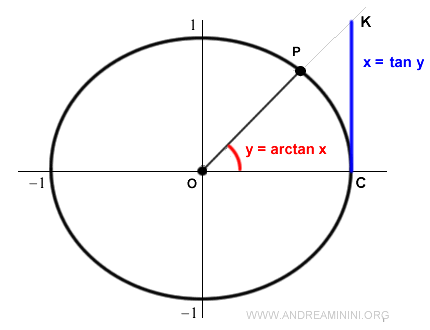
La funzione arcotangente restituisce l'angolo y della tangente.
$$ y = \ arctan \ x $$
Dove x è il valore della tangente
$$ x = \tan y $$
Il grafico dell'arcotangente è il seguente:
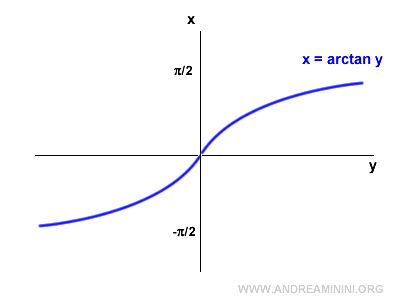
Nota. Il dominio dell'arcotangente è l'insieme dei numeri reali perché coincide con il codominio della tangente. $$ D_{arctan} = ( -\infty ; +\infty ) $$ Il codominio è, invece, l'intervallo [-π/2, π/2].
Un esempio pratico
La tangente di π/4 è 1.
$$ \tan \frac{\pi}{4} = 1 $$
L'arcotangente è la funzione inversa della tangente.
Quindi, l'arcotangente di 1 è π/4.
$$ \arctan 1 = \frac{\pi}{4} $$
Nota. L'arcotangente della tangente è l'argomento della tangente. $$ \arctan (\tan \frac{\pi}{4} )= \frac{\pi}{4} $$
Come costruire il grafico dell'arcotangente
Prendo in considerazione il grafico della tangente.
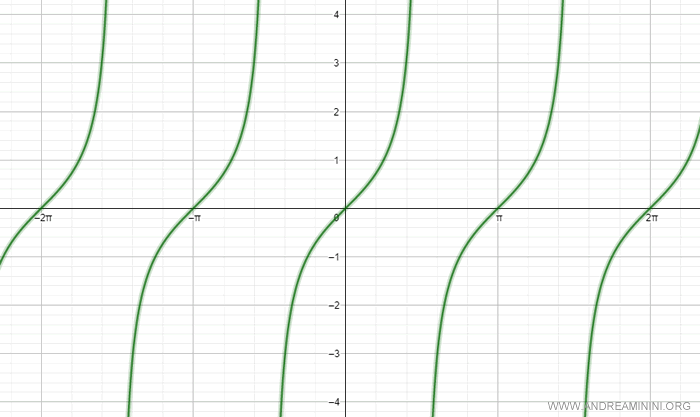
La tangente non è una funzione invertibile perché non è una funzione biunivoca (biettiva).
Per rendere biunivoca la tangente considero una riduzione del dominio nell'intervallo [-π/2, π/2].
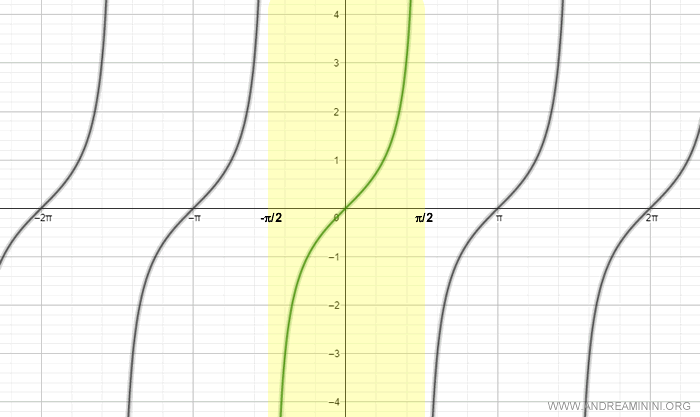
Nell'intervallo [-π/2, π/2] la tangente è una funzione biettiva ed è quindi invertibile.
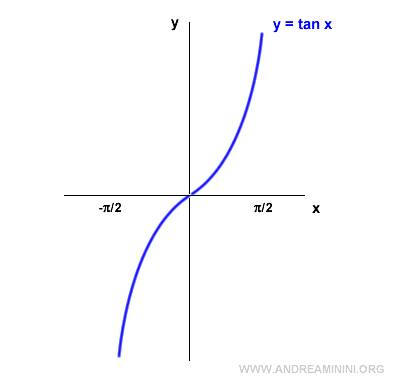
Ruoto il grafico di 90° in senso antiorario.
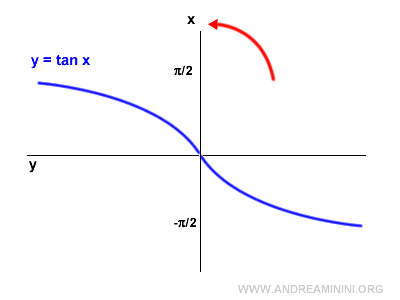
Poi ribalto il grafico in orizzontale con un'operazione di riflessione sull'asse verticale.
Il risultato è il grafico dell'arcotangente.
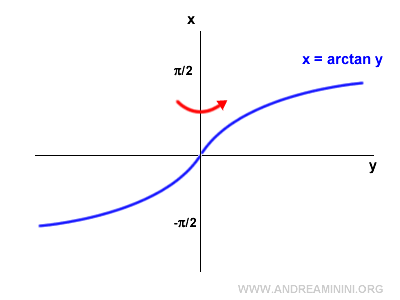
A sua volta l'arcotangente è una funzione invertibile.
La funzione inversa dell'arcotangente è la tangente nell'intervallo [-π/2,π/2].
Nota. Per rendere invertibile la tangente posso scegliere anche intervalli diversi da [-π/2,π/2] dove la funzione tangente è biettiva. Ad esempio [π/2,3π/2]. In questo caso il valore dell'arcotangente è un valore compreso nell'intervallo [π/2,3π/2].
E così via.
