Prima relazione fondamentale della trigonometria
Secondo la prima relazione fondamentale della trigonometria la somma del seno al quadrato e del coseno al quadrato è uguale a 1 $$ \sin^2 \alpha + \cos^2 \alpha = 1 $$
Questa relazione è molto utile perché mi permette di ricavare il seno conoscendo il coseno, e viceversa.
$$ \sin \alpha = \pm \sqrt{1- \cos^2 \alpha } $$
$$ \cos \alpha = \pm \sqrt{1- \sin^2 \alpha } $$
Come si dimostra
La prima relazione fondamentale della trigonometria si dimostra facilmente con il teorema di Pitagora.
Nella circonferenza goniometrica il seno, il coseno e il raggio formano un triangolo rettangolo.
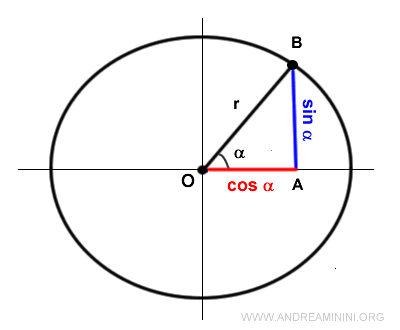
Il seno e il coseno sono i cateti del triangolo mentre il raggio è l'ipotenusa.
Per il teorema di Pitagora la lunghezza dell'ipotenusa è uguale alla radice della somma dei quadrati dei cateti.
$$ r = \sqrt{ \cos^2 \alpha + \sin^2 \alpha } $$
Elevo al quadrato entrambi i membri dell'equazione
$$ r^2 = (\sqrt{ \cos^2 \alpha + \sin^2 \alpha } )^2 $$
$$ r^2 = \cos^2 \alpha + \sin^2 \alpha $$
Sapendo che il raggio della circonferenza goniometrica è uguale a uno (r=1).
$$ 1^2 = \cos^2 \alpha + \sin^2 \alpha $$
Poiché il quadrato di uno è sempre uno.
$$ 1 = \cos^2 \alpha + \sin^2 \alpha $$
Ho ottenuto la prima relazione fondamentale della trigonometria.
$$ \cos^2 \alpha + \sin^2 \alpha = 1 $$
A questo punto posso dimostrare anche le formule correlate del seno e del coseno
Esplicito la funzione seno
$$ \sin^2 \alpha = 1 - \cos^2 \alpha $$
Applico la proprietà invariantiva per calcolare la radice quadrata a entrambi i membri dell'equazione.
$$ \sqrt{ \sin^2 \alpha } = \sqrt{ 1 - \cos^2 \alpha } $$
Poi semplifico.
$$ \sin \alpha = \sqrt{ 1 - \cos^2 \alpha } $$
Ho ottenuto la formula del seno noto il coseno.
Nota. Allo stesso modo posso ricavare la formula del coseno a partire dalla relazione fondamentale della trigonometria. $$ \cos^2 \alpha + \sin^2 \alpha = 1 $$ In questo caso esplicito il coseno. $$ \cos^2 \alpha = 1 - \sin^2 \alpha $$ Calcolo la radice quadrata a entrambi i membri dell'equazione. $$ \sqrt{ \cos^2 \alpha } = \sqrt{ 1 - \sin^2 \alpha } $$ Poi semplifico. $$ \cos \alpha = \sqrt{ 1 - \sin^2 \alpha } $$
La dimostrazione è completa.
E così via.
