Teorema della corda
La lunghezza di una corda in una circonferenza è uguale al diametro per il seno di uno degli angoli che insistono sulla corda. $$ \overline{AB} = 2r \cdot \sin \alpha $$
Dove r è il raggio della circonferenza.
L'angolo alfa è l'angolo compreso tra due segmenti inscritti che collegano gli estremi della corda AB con un punto C qualsiasi della circonferenza.
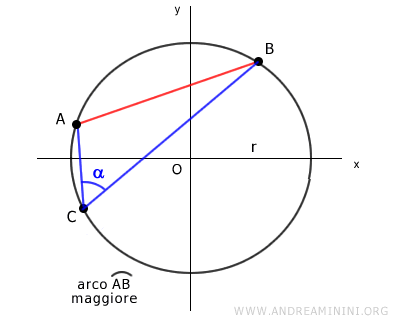
Il teorema della corda è valido sia se il punto C si trova sull'arco maggiore che sull'arco minore della corda.
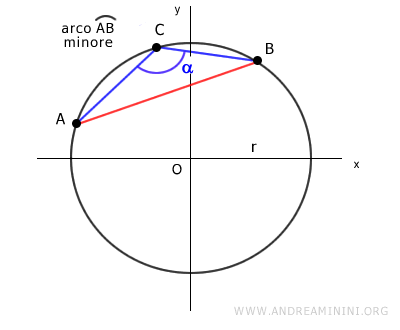
A cosa serve il teorema della corda? Il teorema della corda ha diverse applicazioni. Consente di calcolare la lunghezza di una corda qualsiasi della circonferenza tramite le funzioni trigonometriche. Inoltre, dal teorema della corda derivano altri teoremi utili come il teorema dei seni.
Un esempio pratico
Disegno una circonferenza con raggio r=3
Quindi, il diametro della circonferenza è uguale a sei.
$$ d = 2 \cdot r = 2 \cdot 3 = 6 $$
Scelgo due punti A e B sulla circonferenza.
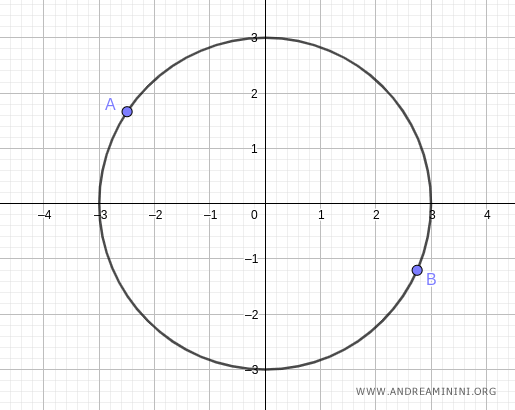
Poi traccio una corda tra due punti A e B.
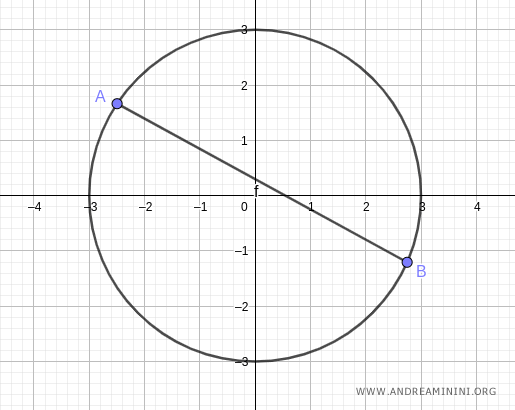
Per determinare la lunghezza della corda applico il teorema trigonometrico della corda.
$$ \overline{AB} = 2r \cdot \sin \alpha $$
Sapendo che il raggio è r=3.
$$ \overline{AB} = 2 \cdot 3 \sin \alpha $$
$$ \overline{AB} = 6 \sin \alpha $$
A questo punto prendo un punto qualsiasi C della circonferenza.
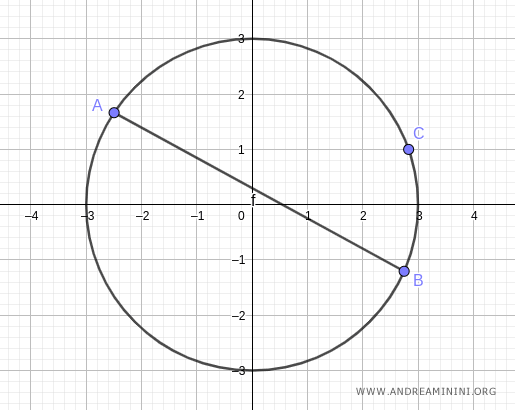
Traccio un segmento AC che collega un estremo della corda con il punto C.
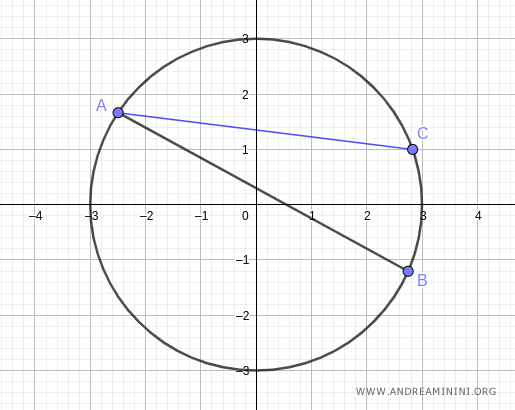
Poi traccio un altro segmento BC che collega l'altro estremo della corda con il punto C.
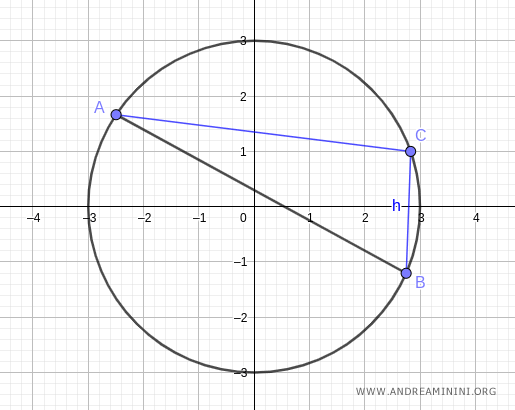
L'angolo ACB formato dai segmenti AC e BC ha un'ampiezza α=95°.
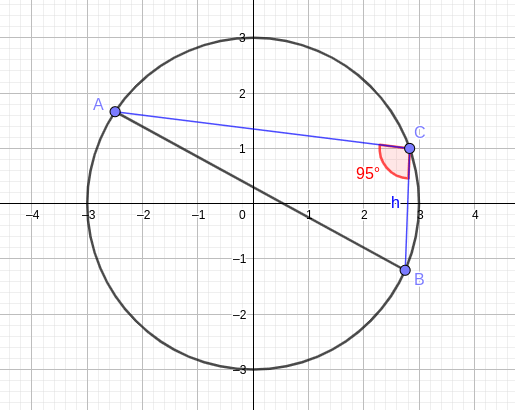
Quindi, per il teorema della corda la lunghezza del segmento AB misura
$$ \overline{AB} = 6 \sin \alpha $$
$$ \overline{AB} = 6 \sin 95° $$
$$ \overline{AB} = 5,98 $$
Pertanto, la lunghezza della corda AB è 5,98.
Nota. Scegliendo un qualsiasi altro punto C della circonferenza il risultato non cambia, perché l'ampiezza dell'angolo alfa è sempre la stessa lungo l'arco AB.
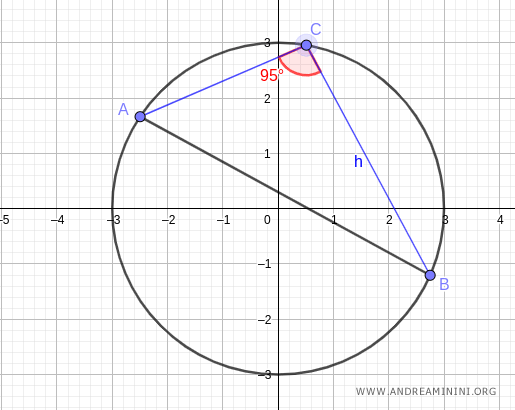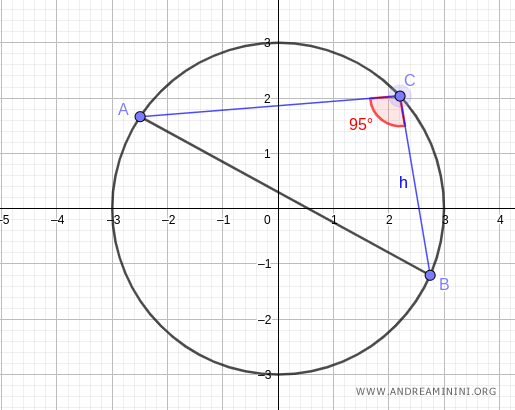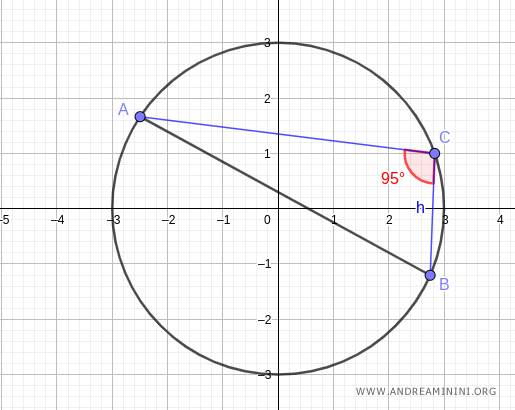
Ad esempio, nell'arco AB superiore l'angolo è 95° mentre nell'angolo inferiore è 85°.
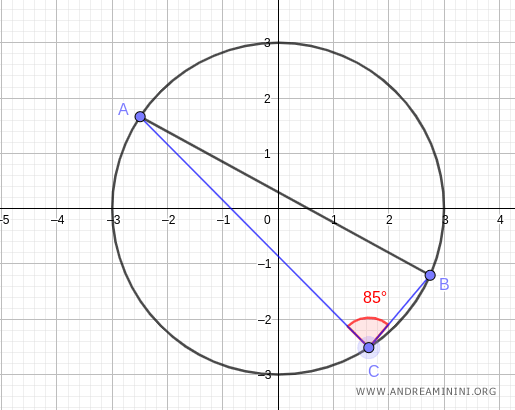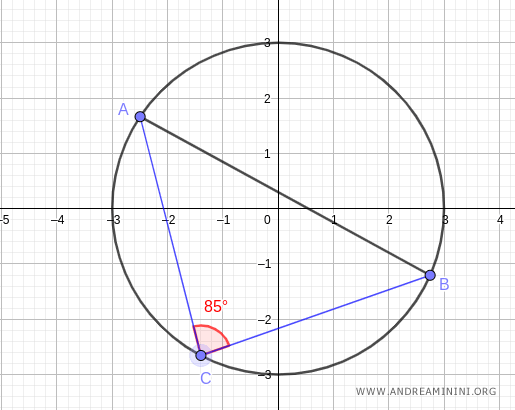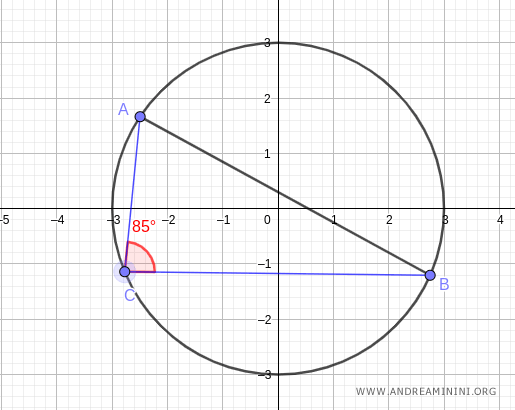
In entrambi i casi, l'angolo resta costante in ogni punto dell'arco e il valore del seno è tale da ottenere la lunghezza della corda AB=5,98.
La dimostrazione
Prendo in considerazione una circonferenza qualsiasi di raggio r.
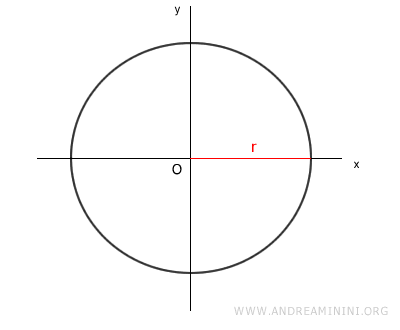
Traccio una corda tra due punti A e B qualsiasi della circonferenza.
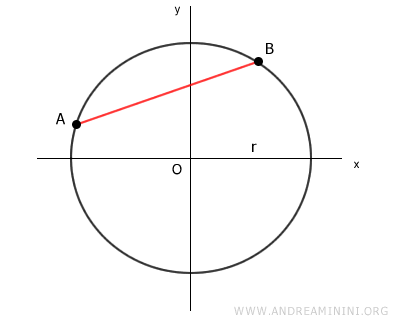
Prendo un punto C qualsiasi nell'arco AB.
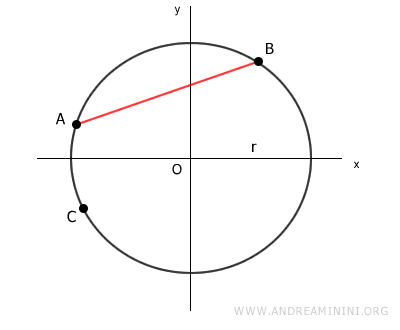
Poi traccio due segmenti AC e BC che collegano il punto C con gli estremi A e B della corda.
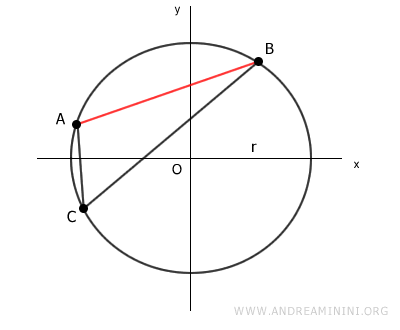
I due segmenti AC e BC formano un angolo ACB di ampiezza alfa
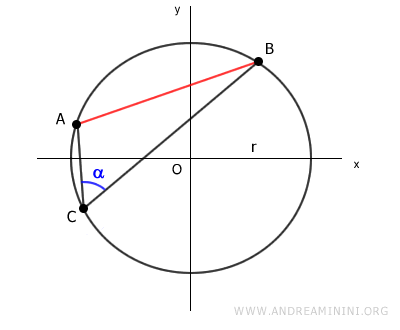
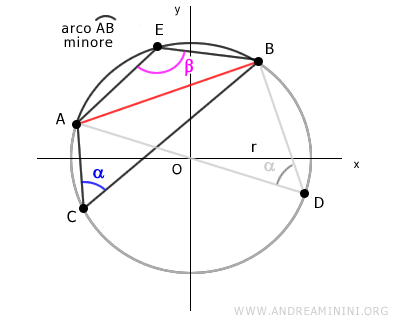
Ora traccio un segmento passante per l'origine O e in uno degli estremi della corda AB.
Ad esempio, il segmento AD.
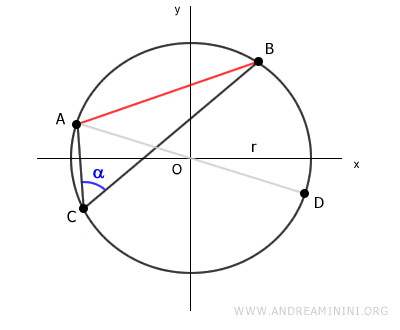
In questo modo individuo un altro punto D della circonferenza.
A questo punto unisco il punto D con l'altro estremo (B) della corda AB.
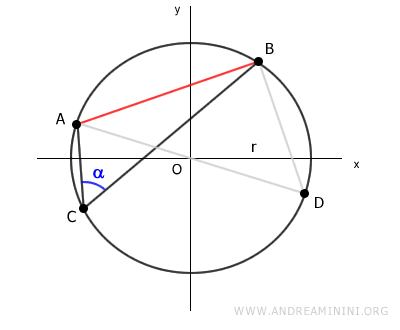
Ottengo un altro triangolo ABD.
Il triangolo ABD è un triangolo rettangolo perché è inscritto nella semicirconferenza AD.
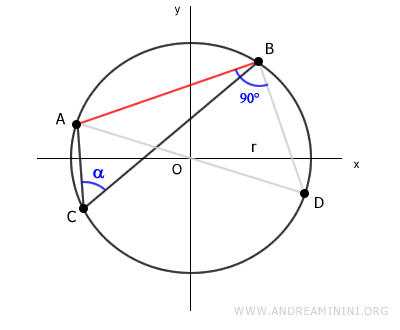
I due triangoli ABC e ABD insistono sullo stesso arco AB.
Quindi, l'angolo ADB è congruente con l'angolo alfa.
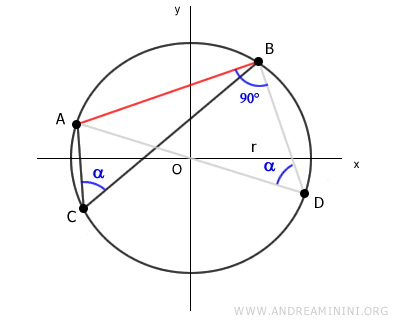
Il triangolo ADB è un triangolo rettangolo.
Quindi, posso applicare il primo teorema del triangolo rettangolo per ottenere la lunghezza del segmento AB.
$$ \overline{AB} = \overline{AD} \cdot \sin \alpha$$
Nota. Secondo il primo teorema del triangolo rettangolo, un cateto è uguale all'ipotenusa per il seno dell'angolo opposto. In questo caso, il cateto del triangolo ADB è il segmento AB che voglio calcolare, l'ipotenusa è il segmento AD mentre l'angolo opposto rispetto al segmento AB è l'angolo alfa.
Il segmento AD è il diametro della circonferenza, ossia due volte il raggio AD=2r
$$ \overline{AB} = 2r \cdot \sin \alpha$$
Questo dimostra la formula del teorema della corda sull'arco AB maggiore.
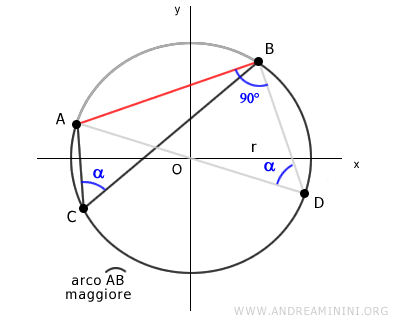
Ora devo dimostrare che il teorema è ancora valido anche se considero un punto sull'altro arco AB minore.
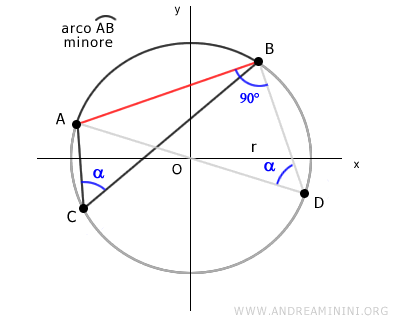
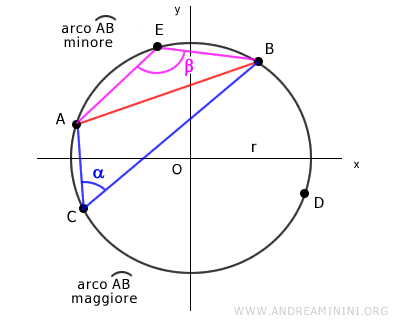
Prendo un punto E qualsiasi nell'arco AB minore.
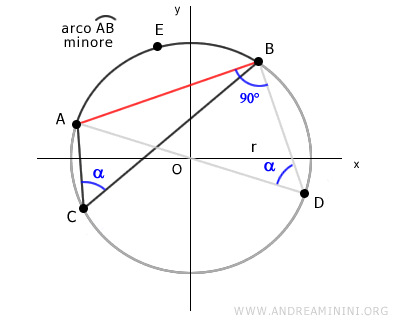
Poi congiungo il punto E agli estremi A e B della corda.
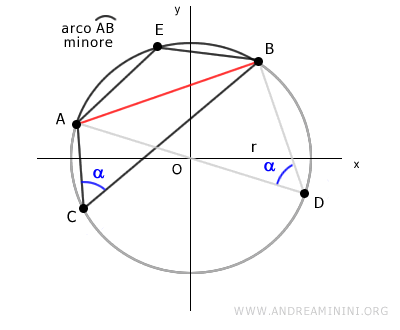
In questo modo ottengo un quadrilatero AEBC dove i segmenti AE e BE formano un angolo di ampiezza β.
Gli angoli opposti α e β del quadrilatero sono angoli supplementari perché il quadrilatero è inscritto nella circonferenza.
Quindi la loro somma è pari a 180° ossia pi greco π radianti
$$ \alpha + \beta = \pi $$
L'angolo alfa α lo conosco già.
Pertanto metto in evidenza l'angolo beta β.
$$ \beta = \pi - \alpha $$
Applico il seno a entrambi i membri dell'equazione
$$ \sin \beta = \sin \pi - \alpha $$
Per la proprietà trigonometrica degli angoli associati vale l'uguaglianza sin(π-α)=sin(α)
$$ \sin \beta = \sin \pi - \alpha = \sin \alpha $$
Questo vuol dire che sin(β)=sin(α)
Quindi, il teorema della corda che ho dimostrato precedentemente sull'arco maggiore AB
$$ \overline{AB} = 2r \cdot \sin \alpha$$
posso ottenerlo anche utilizzando l'angolo beta sull'arco minore AB
$$ \overline{AB} = 2r \cdot \sin \alpha = 2r \cdot \sin \beta $$
Questo dimostra il teorema della corda su entrambi gli archi AB.
E così via.
