Il confine è un sottoinsieme dell'insieme A se e solo se A è chiuso

Il confine \( \partial A \) dell'insieme \( A \) è un sottoinsieme di \( A \) se e solo se \( A \) è chiuso. \[ \partial A \subseteq A \Leftrightarrow A \text{ è chiuso} \]

Esempio pratico

Esempio 1

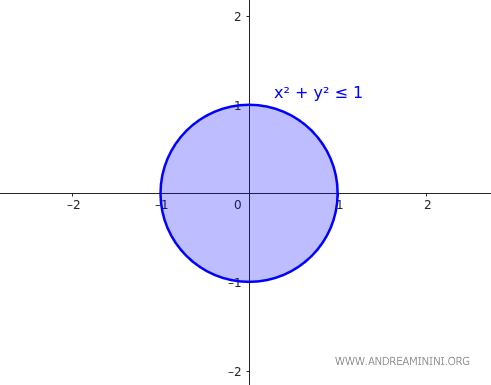
L'insieme \( A \) è un cerchio chiuso di raggio 1 centrato nell'origine nello spazio euclideo \(\mathbb{R}^2\).

$$ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 $$

Il bordo di \( A \) in questo caso è la circonferenza di raggio 1:

$$ \partial A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1  $$

Poiché \( A \) è un cerchio chiuso, contiene tutti i suoi punti di accumulazione. In particolare, contiene tutti i punti del suo bordo:

$$ \partial A \subseteq A $$

Quindi, \( A \) è chiuso.

Esempio 2

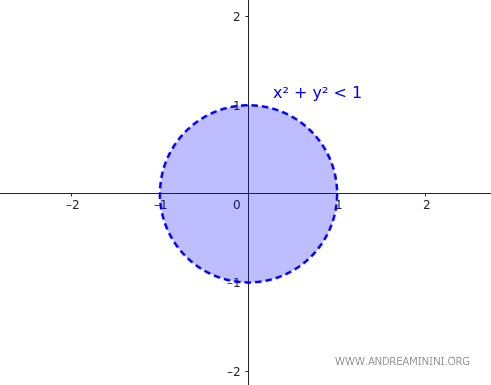
L'insieme \( B \) è un cerchio aperto di raggio 1 centrato nell'origine:

$$ B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 $$

Il bordo di \( B \) è ancora la circonferenza di raggio 1:

$$ \partial B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 $$

Tuttavia, in questo caso, \( B \) non contiene il suo bordo, perché \( B \) è definito come il cerchio aperto, quindi:

$$ \partial B \nsubseteq B $$

Questo dimostra che \( B \) non è chiuso.

Questi esempi mostrano chiaramente come un insieme chiuso contenga il proprio bordo, mentre un insieme aperto no.

Dimostrazione

Divido la dimostrazione in due parti

1] Se il confine di A è un sottoinsieme di A allora l'insieme A è chiuso

Considero per ipotesi che \( \partial A \subseteq A \) il confine di \( A \) sia un sottoinsieme di \( A \).

Devo dimostrare che l'insieme \( A \) è chiuso.

Il bordo di \( A \) è definito come \( \partial A = \overline{A} \cap \overline{A^c} \), dove \( \overline{A} \) è la chiusura di \( A \) e \( \overline{A^c} \) è la chiusura del complementare di \( A \).

Se il confine di \( A \) è un sottoinsieme \( \partial A \subseteq A \), allora ogni punto di \( \partial A \) è anche in \( A \).

Tuttavia, per definizione del bordo, ogni punto di \( \partial A \) è anche un punto di accumulazione di \( A \) o di \( A^c \).

Per avere \( \partial A \subseteq A \), \( A \) deve contenere tutti i suoi punti di accumulazione, il che significa che \( A \) è chiuso perché per definizione di insieme chiuso, un insieme è chiuso se contiene tutti i suoi punti di accumulazione.

2] Se l'insieme A è chiuso, allora il suo confine è un sottoinsieme di A

Per ipotesi iniziale l'insieme \( A \) è chiuso. Devo dimostrare che \( \partial A \subseteq A \) il suo confine è un sottoinsieme di \( A \).

Se \( A \) è chiuso, allora è uguale alla sua chiusura $ \text{Cl}(A) $

$$ A = \text{Cl}(A) $$

Il bordo di \( A \) è l'intersezione tra la chiusura di \( A \) e la chiusura del suo insieme complementare \( A^c \)

$$ \partial A = \text{Cl}(A) \cap \text{Cl}(A^c) $$

Sapendo che \( \text{Cl}(A) = A \) in quanto \( A \)  è chiuso

$$ \partial A = A \cap \text{Cl}(A^c) $$

Il termine \( A \cap \text{Cl}(A^c) \) rappresenta i punti che sono sia in \( A \) sia nella chiusura del complementare di \( A \).

Tuttavia, se \( A \) è chiuso, l'intersezione \( A \cap \text{Cl}(A^c) \) contiene solo i punti che appartengono al bordo di \( A \).

Quindi, se \( A \) è chiuso, il bordo \( \partial A \) è contenuto in \( A \).

3] Conclusione

In conclusione, ho dimostrato che \( \partial A \subseteq A \) se e solo se \( A \) è chiuso.

E così via.