Il teorema del confine di un insieme

Un punto $ x $ appartiene al confine di un insieme $ A $ se ogni volta che prendo un intorno di $ x $, questo interseca sia l'insieme $ A $ sia tutto quello che non è $ A $ (cioè $ X - A $).

In altre parole, se non riesco a trovare un intorno di $ x $ che stia tutto dentro $ A $ o tutto fuori da $ A $, allora $ x $ sta sul confine di $ A $.

Un esempio pratico
La dimostrazione

Un esempio pratico

Faccio un esempio pratico per capire meglio.

Considero l'insieme $ A = (0, 1) $ sulla retta reale $ \mathbb{R} $.

I punti 0 e 1 sono sul confine di $ A $ perché ogni volta che prendo un intorno di 0 o 1, questo ha sempre una parte dentro $ (0, 1) $ e una parte fuori $ (0, 1) $.

Punto 1
Un qualsiasi intorno $ (1-\epsilon, 1+\epsilon) $ con ε infinitamente piccolo ha una parte (1-ε,1) compresa tra (0,1) e una parte (1,1+ε) al di fuori di (0,1). Quindi, il punto 1 è un punto di confine dell'insieme A.
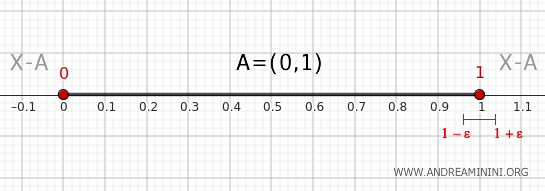
Punto 0
Un qualsiasi intorno $ (0-\epsilon, 0+\epsilon) $ con ε infinitamente piccolo ha una parte (0,0+ε) compresa tra (0,1) e una parte (0-ε,0) al di fuori di (0,1). Quindi, il punto 0 è altro un punto di confine dell'insieme A.
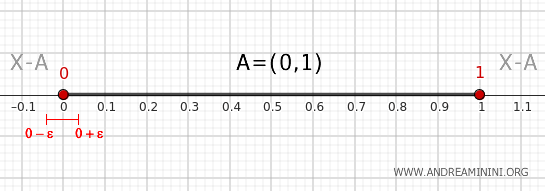
Punto nell'intervallo (0,1)
Ogni punto x dentro l'insieme ha un intorno (x-ε,x+ε) con ε infinitamente piccolo che appartiene a A=(0,1) ma non appartiene a X-A. Quindi, i punti interni dell'intervallo (0,1) non sono punti di confine.
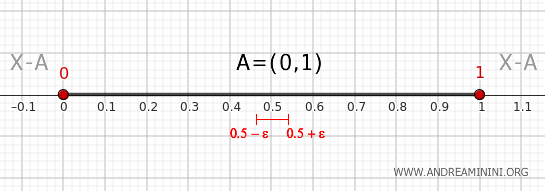
Punto al di fuori dell'intervallo (0,1)
Ogni punto esterno all'intervallo (0,1), purché diverso da 0 e da 1, ha un intorno (x-ε,x+ε) con ε infinitamente piccolo che è compreso in X-A ma non è compreso in A=(0,1). Quindi, i punti esterni di [0,1] non sono punti di confine di A.

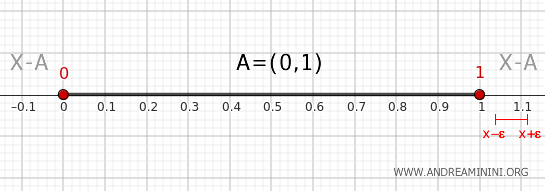
Pertanto, i punti di confine dell'insieme $ A $ sono i punti 0 e 1.

$$ \partial A = \{0,1 \} $$

Quindi, in sintesi, un punto $ x $ è sul confine di $ A $ se non riesco mai a trovare un intorno che stia tutto dentro $ A $ o tutto fuori $ A $. Chiaro adesso?

La dimostrazione

Per dimostrare il teorema prendo in considerazione due ipotesi:

1] Il punto x è un punto del confine di A

Considero un punto $ x $ nel confine dell'insieme $ A $

$$ x \in \partial A $$

Questo implica che $ x \in \text{Cl}(A) $ e $ x \notin \text{Int}(A) $.

Poiché $ x \in \text{Cl}(A) $, ogni intorno di $ x $ interseca $ A $.

Inoltre, poiché $ x \notin \text{Int}(A) $, ogni intorno di $ x $ non è un sottoinsieme di $ A $ e quindi deve intersecare $ X - A $.

Pertanto, ogni intorno di $ x $ interseca sia $ A $ che $ X - A $.

2] Il punto x interseca sia A che X-A

Suppongo ora che ogni intorno del punto $ x $ interseca sia $ A $ che $ X - A $.

Ne consegue che il punto appartenga a entrambi gli insiemi $ x \in \text{Cl}(A) $ e $ x \in \text{Cl}(X - A) $.

Dato che $ \text{Cl}(X - A) = X - \text{Int}(A) $, deduco che $ x \notin \text{Int}(A) $.

Pertanto, $ x \in \text{Cl}(A) $ e $ x \notin \text{Int}(A) $, ovvero $ x \in \text{Cl}(A) - \text{Int}(A) = \partial A $.

Questo dimostra che il punto $ x $ è un punto del confine di $ A $

E così via.