Teorema di Rolle

In una funzione f(x) continua e derivabile in un intervallo (a,b), se f(a)=f(b) esiste sempre un punto x₀ in (a,b) per cui la derivata prima è f'(x₀)=0.

Dimostrazione

Data una funzione continua in [a,b] e derivabile in (a,b), per ipotesi esiste un punto di minimo (x₁) e di massimo (x₂)

$$ f(x_1) \le f(x) \le f(x_2) $$

Per dimostrare l'esistenza di una derivata nulla esamino i due casi possibili

1) Minimo/massimo intermedio nell'intervallo

Se almeno uno dei due punti di massimo (x₂) e/o minimo (x₁) è un punto intermedio nell'intervallo (a,b), secondo il teorema di Fermat tale punto ha derivata nulla.

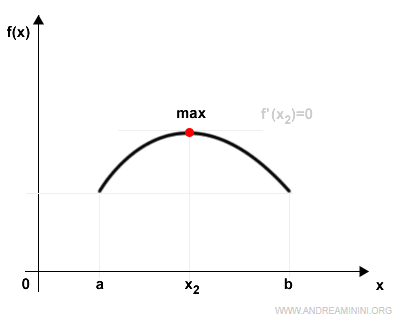
Pertanto, almeno un punto x della funzione f(x) nell'intervallo (a,b) ha derivata nulla.

2] Minimo/massimo estremi nell'intervallo

Se invece i due punti di minimo (x₁) e di massimo (x₂) sono punti estremi dell'intervallo, ossia non sono interni

$$ f(x_1)=f(a) \\ f(x_2)=f(b) $$

Poiché per ipotesi iniziale la funzione f(x) ha lo stesso valore agli estremi

$$ f(a)=f(b) $$

allora il minimo e il massimo hanno lo stesso valore f(x)

$$ f(x_1)=f(x_2) $$

Essendo il minimo e il massimo uguali, questo vuol dire che la funzione f(x) è uguale agli estremi e costante in ogni punto dell'intervallo (a,b)

$$ f(x_1) \le f(x) \le f(x_2) $$

$$ f(x_1) = f(x) = f(x_2) $$

Se la funzione f(x) è costante in ogni punto x dell'intervallo (a,b), allora in ogni punto x la derivata prima f'(x) è nulla.

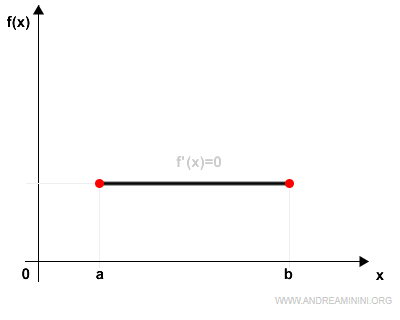
In questo caso esistono infiniti punti con derivata nulla f(x)=0 nell'intervallo (a,b).

Ho così dimostrato la presenza di almeno una derivata nulla f'(x) nell'intervallo (a,b) se f(a)=f(b).

E così via.