Il teorema delle rette parallele

Quindi, per affermare che due rette sono parallele è sufficiente che una delle ipotesi sia soddisfatta. Se una delle ipotesi è soddisfatta, lo sono anche le altre.

Questo teorema è anche noto come criterio di parallelismo.

Nota. Vale anche il teorema inverso, ossia se due rette sono parallele, allora formano con una trasversale coppie di angoli alterni (interni o esterni) congruenti, coppie di angoli corrispondenti congruenti e coppie di angoli coniugati (interni o esterni) supplementari. Quindi, i due teoremi sono una condizione necessaria e sufficiente per il parallelismo di due rette.

Dimostrazione

Date due rette r e s e una terza retta trasversale, devo stabilire se le rette r e s sono parallele oppure no.

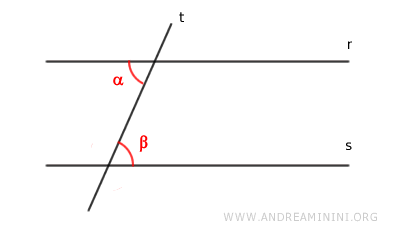
Considero come ipotesi iniziale la congruenza di due angoli alterni interni.

$$ \alpha \cong \beta $$

Poi, per assurdo, ipotizzo che le due rette si incontrino in un punto C.

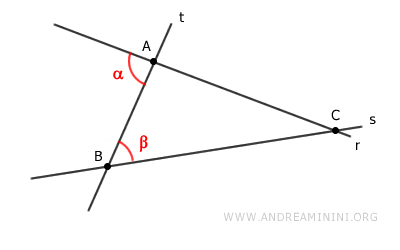
Se così fosse, le due rette e la retta trasversale formerebbero un triangolo ABC.

In base al teorema dell'angolo esterno di un triangolo, l'angolo esterno α ha un'ampiezza maggiore rispetto agli angoli interni non adiacenti.

Quindi, l'angolo esterno α è maggiore dell'angolo interno β.

$$ \alpha > \beta $$

Così facendo, però, viene contraddetta l'ipotesi iniziale della congruenza α≅β degli angoli alterni interni.

Pertanto, la tesi che due rette r e s tagliate da una trasversale con angoli alterni interni congruenti (α≅β) si incontrano in un punto C è falsa.

Se questa tesi è falsa, è vero il suo contrario: due rette con angoli alterni interni congruenti NON si incontrano in un punto C.

Sapendo che se due rette non si intersecano, allora sono rette parallele, posso concludere che due rette r e s tagliate da una trasversale con angoli alterni interni congruenti (α≅β) sono rette parallele.

La tesi è dimostrata per gli angoli alterni interni congruenti.

Tutte le altre ipotesi tra gli angoli sono riconducibili alla congruenza degli angoli alterni interni.

• Angoli alterni esterni congruenti
  Se gli angoli alterni esterni sono congruenti (α≅β), sapendo che questi sono opposti al vertice rispetto agli angoli alterni interni (α≅α') e (β≅β'), allora anche gli angoli alterni interni sono congruenti (α'≅β').
  
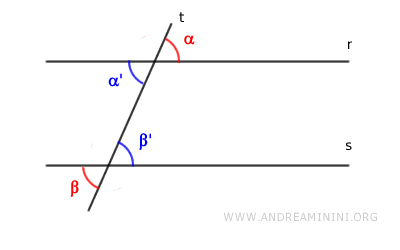
• Angoli corrispondenti congruenti
  Se gli angoli corrispondenti sono congruenti (α≅β), sapendo che ogni angolo è congruente con l'angolo opposto al vertice (β≅β'), allora sono congruenti anche gli angoli alterni interni (α≅β').
  
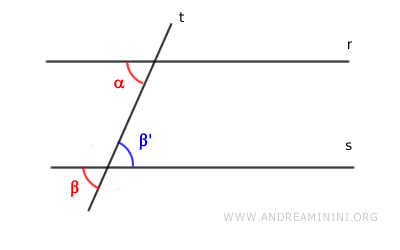
• Angoli coniugati supplementari
  Se gli angoli coniugati sono supplementari (α+β=180°), sapendo che anche gli angoli adiacenti sulla retta r e s sono supplementari (α+β'=180°), allora gli angoli alterni interni sono congruenti (α≅β').
  

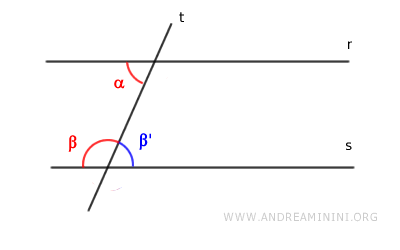
Una volta ricondotto il problema al caso degli angoli alterni interni congruenti, non devo fare altro perché la tesi è già stata dimostrata.

Il teorema inverso delle parallele

La dimostrazione

In questo caso l'ipotesi iniziale è che due rette siano parallele

$$ r // s $$

Devo dimostrare che esistono due angoli alterni interni congruenti α≅β.

Anche in questo caso seguo un ragionamento per assurdo.

Parto dall'ipotesi che due rette parallele abbiano angoli alterni interni non congruenti. Ad esempio α>β

$$ \alpha > \beta $$

Ora la situazione si presenta in questo modo.

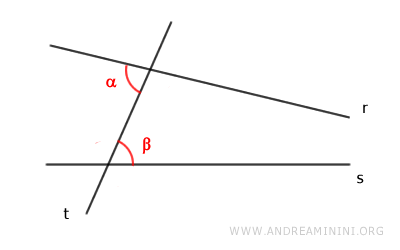
Pertanto, posso tracciare una ulteriore retta r' che abbia un angolo alterno interno α' congruente con β ossia α'≅β.

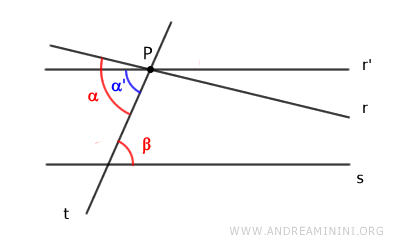
In questo caso però esistono due rette parallele a s che passano per il punto P.

• Le rette r // s sono parallele per l'ipotesi iniziale
• Le rette r' // s sono parallele per il teorema delle parallele, perché hanno una coppia di angoli alterni congruenti α'≅β

L'esistenza di due rette parallele alla retta s che passano per lo stesso punto P contraddice il postulato delle parallele

Secondo il postulato delle parallele deve esistere una e una sola retta parallela a s che passa per il punto P.

Quindi, l'affermazione che due rette parallele r e s abbiano angoli alterni interni non congruenti è falsa.

Di consequenza, è vera l'affermazione contraria: due rette parallele r e s hanno angoli alterni interni congruenti (α≅β).

In questo modo ho dimostrato il teorema nel caso degli angoli alterni interni congruenti.

Anche in questo caso posso ricondurre tutte le altre situazioni (es. angoli alterni esteri congruenti, angoli corrispondenti congruenti, angoli coniugati interni/esterni supplementari) al caso degli angoli alterni interni congruenti. Pertanto, questa dimostrazione vale per tutti i casi.

Osservazioni

Alcune osservazioni sul teorema delle rette parallele

• Corollario

  Se due rette, r e s, sono entrambe perpendicolari a una terza retta t, allora esse sono parallele tra loro.
  

  Questo perché, quando due rette sono perpendicolari alla stessa retta, creano angoli corrispondenti di 90° che sono congruenti. In base al teorema delle rette parallele, questo implica che le due rette siano parallele.

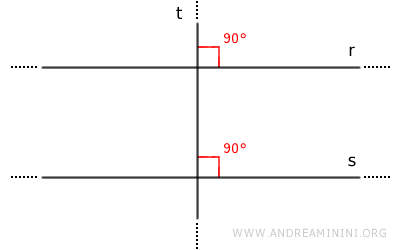
  Nota. Allo stesso modo potrei anche osservare che le rette r e s formano coppie di angoli alterni interni (o esterni) congruenti oppure coppie di angoli coniugati che sono supplementari (180°). In ogni caso, la deduzione logica che ne deriva è che le rette r e s sono parallele.

• Date due rette parallele r e s, se la retta t è perpendicolare a una di esse, allora è perpendicolare anche all'altra.
  

  Dimostrazione. Considero due rette parallele r//s e una terza retta t perpendicolare alla retta s. Le rette t e s formano un angolo α=90°.
  
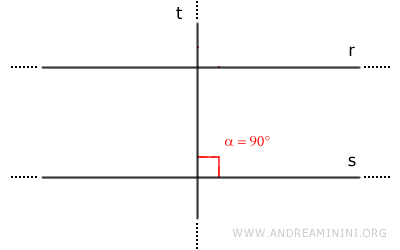
  Essendo due rette parallele r//s, per il teorema delle rette parallele le rette r e s formano coppie di angoli corrispondenti congruenti rispetto a una trasversale. Quindi, anche l'angolo β è un angolo retto (β=90°).
  
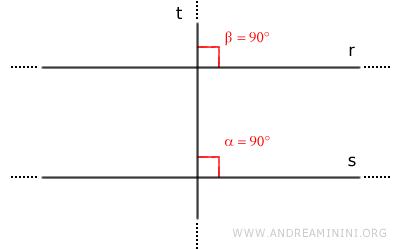
  Di conseguenza, la retta t è perpendicolare anche alla retta r.

E così via.