Angoli esterni

Gli angoli esterni sono angoli formati dall'intersezione di un lato del poligono e il prolungamento di un lato adiacente.

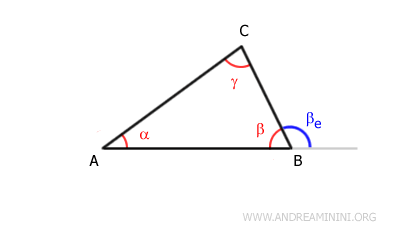
Ad esempio, considero il triangolo ABC.

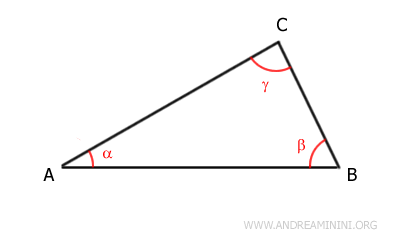
Il triangolo ha tre angoli interni α, β e γ.

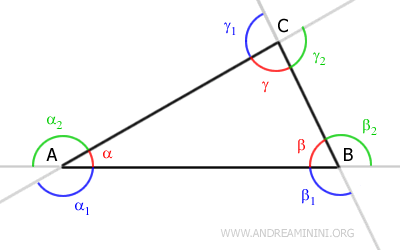
Il triangolo ha i seguenti angoli esterni che misuro seguendo l'ordine antiorario:

• L'angolo α₁ è tra il prolungamento del lato AC e il lato AB
• L'angolo α₂ è tra il lato AC e il prolungamento del lato AB
• L'angolo β₁ è tra il lato AB e il prolungamento del lato BC
• L'angolo β₂ è tra il prolungamento del lato AB e il lato BC
• L'angolo γ₁ è tra il prolungamento del lato BC e il lato AC
• L'angolo γ₂ è tra il lato BC e il prolungamento del lato AC

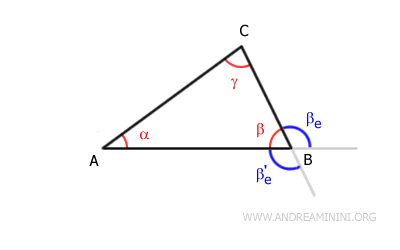
Ogni angolo interno ha due angoli esterni adiacenti. Ad esempio, l'angolo interno β ha due angoli esterni adiacenti β_e e β_e'

Le osservazioni

Alcune osservazioni utili sulla somma degli angoli

• Somma degli angoli esterni
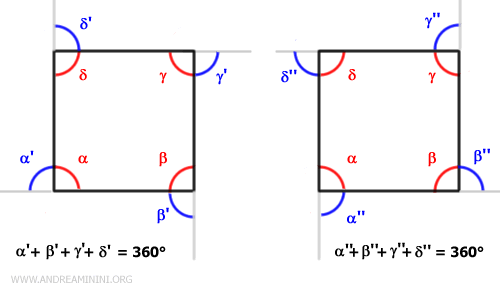
  La somma degli angoli esterni di un poligono è sempre 360°, a prescindere dal numero dei suoi lati.

  Esempio. Un quadrato ha 4 lati e 4 angoli interni di 90°. Sebbene ogni angolo presenti due angoli esterni adiacenti, in un dato momento possiamo considerare soltanto 4 angoli esterni in totale, uno per ciascun vertice. La somma di questi angoli esterni è costantemente pari a 360°.
  

• Teorema dell'angolo esterno
  In un triangolo ogni angolo esterno è maggiore di ciascuno degli angoli interni non adiacenti.

  Esempio. Nel triangolo ABC l'angolo esterno β_e è maggiore di ciascuno degli angoli interni che non gli sono adiacenti: α e γ.
  
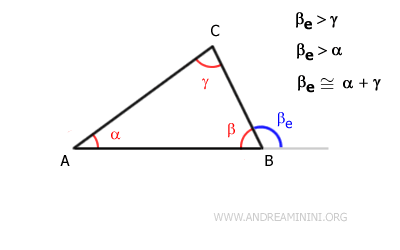
  L'angolo interno β non va considerato perché è adiacente all'angolo esterno β_e.

• La relazione tra angoli interni ed esterni
  In un poligono qualsiasi, la somma di un angolo interno con un angolo esterno adiacente è sempre uguale a un angolo piatto di 180°.

  Esempio. Nel triangolo ABC la somma dell'angolo interno β con l'angolo esterno β_e forma un angolo piatto (180°),
  

E così via.