Il primo principio di equivalenza delle equazioni

In base al primo principio di equivalenza delle equazioni, se aggiungo o sottraggo lo stesso valore o espressione k a entrambi i membri di un'equazione, ottengo un'equazione equivalente. $$ a = b \ \ \Leftrightarrow a+k = b+k $$

In altre parole, se ho un'equazione del tipo

$$ a = b $$

Posso sommare lo stesso valore o espressione a entrambi i membri dell'equazione, ottenendo ancora un'equazione equivalente.

$$ a + k = b + k $$

Allo stesso modo ottengo una equazione equivalente se sottraggo lo stesso valore o espressione a entrambi i membri.

$$ a - k = b - k $$

Nota. Due o più equazioni sono tra loro equivalenti se hanno lo stesso insieme di soluzioni.

A cosa serve il primo principio di equivalenza?

Questo principio è molto utile perché mi permette di semplificare un'equazione e renderla più facilmente risolvibile.

Un esempio pratico

Considero l'equazione

$$ 8x + 5 = 13x - 7 $$

Applico il primo principio di equivalenza delle equazioni sottraendo 8x ad entrambi i membri dell'equazione

$$ 8x + 5 \color{red}{-8x} = 13x - 7 \color{red}{-8x} $$

In questo modo annullo il termine 8x al primo membro e lo sposto al secondo membro cambiato di segno.

Dopo la semplificazione ottengo

$$ 5 = 13x - 7 - 8x $$

Questo mi permette di sottrarre 13x - 8x tra loro

$$ 5 = 5x - 7 $$

A questo punto posso applicare nuovamente il primo principio di equivalenza sommando 7 a entrambi i membri.

$$ 5 \color{red}{+7} = 5x - 7 \color{red}{+7} $$

Questo mi permette di spostare il termine -7 al primo membro cambiato di segno e di sommarlo con 5.

$$ 12 = 5x $$

In questo modo, ho semplificato l'equazione iniziale e reso più facile la sua risoluzione.

Nota. Il primo principio di equivalenza è un analogo matematico della bilancia in fisica. Se ho una bilancia in pareggio e aggiungo o tolgo lo stesso peso in entrambi i piatti, la bilancia resta in pareggio. Lo stesso accade in un'equazione.

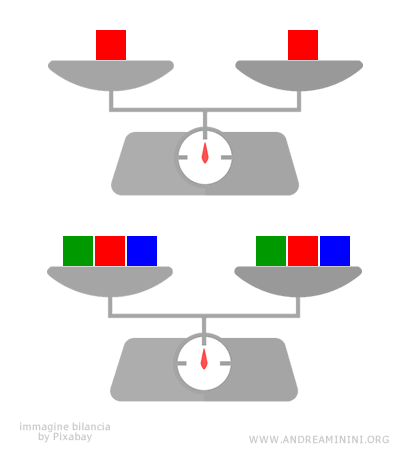
E così via