Le matrici equivalenti
Due matrici sono equivalenti quando i sistemi lineari associati hanno lo stesso insieme delle soluzioni S.
Esempio

Il rapporto di equivalenza tra due matrici M e M' è indicato con il simbolo della tilde.
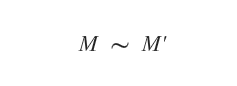
Un esempio pratico
Una matrice è associata a un sistema di equazioni lineari.

Se in un sistema lineare modifico l'ordine delle equazioni, il risultato del sistema lineare non cambia.
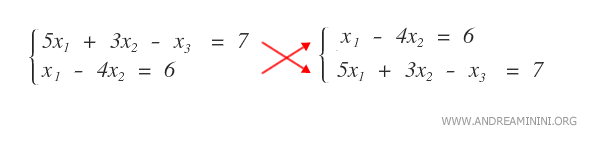
Allo stesso modo, se modifico l'ordine delle righe di una matrice, il risultato è sempre lo stesso.

Nota. Si tratta soltanto di un esempio banale per rendere l'idea. In realtà, oltre a modificare l'ordine delle righe, le matrici equivalenti possono anche avere elementi con valori completamente diversi tra loro. Esistono diversi metodi e algoritmi di trasformazione. I più noti sono quelli di Gauss e di Gauss-Jordan.
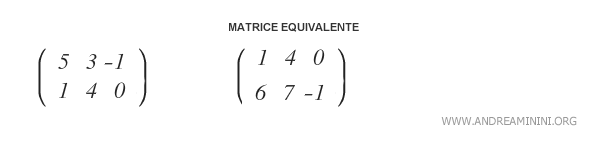
Come costruire una matrice equivalente
Secondo il metodo di eliminazione di Gauss, qualsiasi matrice M può essere trasformata in una matrice equivalente M' tramite una serie di operazioni ammissibili dette mosse di Gauss.
- scambio di posto tra due righe della matrice
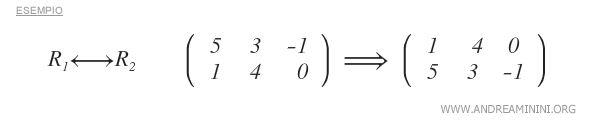
- prodotto di una riga per numero reale α diverso da zero
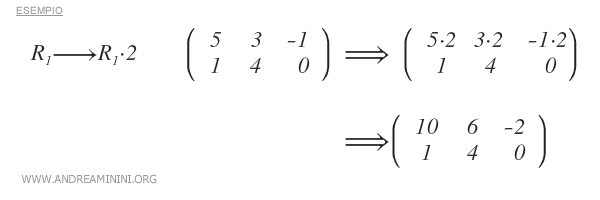
- somma degli elementi corrispondenti tra due righe
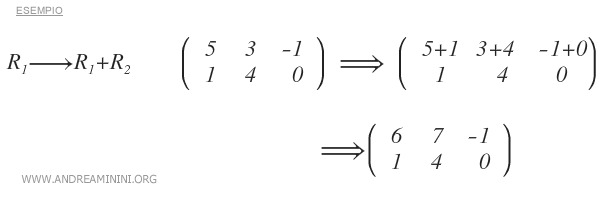
Se due polinomi hanno uno zero, questo resta anche nel polinomio della somma. Quindi, la soluzione di entrambi i polinomi è una soluzione anche nel polinomio della somma.
Nota. Le operazioni si possono compiere anche contemporaneamente. Ad esempio, si può sommare una riga con il prodotto di un'altra riga per un numero reale.
