La matrice ortogonale
Una matrice A è detta ortogonale quando la sua matrice inversa A-1 è uguale alla matrice trasposta AT.

L'insieme delle matrici ortogonali di ordine n è indicato con il simbolo On.
Nota. Soltanto le matrici invertibili possono essere ortogonali. Quindi, le matrici ortogonali sono un sottoinsieme On dell'insieme GLn(R) delle matrici quadrate invertibili di ordine n.
Nelle matrici ortogonali il prodotto della matrice A per la matrice trasposta AT è uguale alla matrice identità In di ordine n.

Dimostrazione
La dimostrazione è molto semplice, una delle proprietà delle matrici invertibili è la seguente:

Nelle matrici ortogonali la matrice inversa è uguale alla matrice trasposta ( A-1=AT ).
Quindi si può affermare che AAT=In.
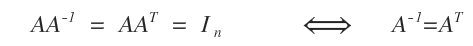
Un esempio pratico
La seguente matrice quadrata è una matrice ortogonale.

Per averne la prova è sufficiente moltiplicare A per la sua matrice trasposta AT.
Il prodotto di A·AT è uguale alla matrice identità I2.

Da ciò si deduce che AT=A-1.

Perché? E' una proprietà delle matrici inverse. Il prodotto di una matrice invertibile (A) per la sua matrice inversa (A-1) dà come risultato una matrice unitaria I. Quindi, se AAT=I e AA-1=I allora AT=A-1.
Questo dimostra che si tratta effettivamente di una matrice ortogonale.
I gruppi O e SO delle matrici ortogonali
Tutte le matrici ortogonali formano un gruppo, detto gruppo ortogonale e indicato con \( O(n) \), perché soddisfano le quattro condizioni fondamentali dell'algebra astratta che definiscono un gruppo:
- Chiusura: il prodotto di due matrici ortogonali è ancora una matrice ortogonale;
- Associatività: il prodotto tra matrici è associativo;
- Elemento neutro: la matrice identità \( I \) appartiene a \( O(n) \) e funge da elemento neutro;
- Elemento inverso: ogni matrice ortogonale \( A \) ha come inversa la sua trasposta \( A^{T} \), anch’essa ortogonale.
Di conseguenza, l’insieme di tutte le matrici reali \( A \) tali che:
$$ A^{T}A = AA^{T} = I $$
costituisce un gruppo rispetto all’operazione di moltiplicazione tra matrici.
Il gruppo ortogonale \( O(n) \) rappresenta tutte le trasformazioni isometriche lineari che preservano lunghezze e angoli nello spazio euclideo, come le rotazioni e le riflessioni.
Nota. In due dimensioni, una matrice ortogonale appartenente al gruppo $ O(2) $ può rappresentare una rotazione o una riflessione del piano. In tre dimensioni, invece, le matrici ortogonali del gruppo $ O(3) $ descrivono rotazioni e simmetrie dello spazio, cioè tutte le trasformazioni che mantengono invariata la struttura geometrica dello spazio tridimensionale.
Pertanto, il gruppo O(n) include dunque tutte le rotazioni e le riflessioni possibili in uno spazio di n dimensioni.
Tuttavia, non tutte queste trasformazioni conservano l’orientamento: alcune, come le riflessioni, lo invertono.
Per questo motivo, al suo interno si distingue un sottogruppo molto importante, il gruppo speciale ortogonale $ SO(n) $, formato da tutte le matrici ortogonali con determinante uguale a +1:
$$ SO(n) = \{ A \in O(n) \;|\; \det(A) = +1 \} $$
Le matrici appartenenti a SO(n) rappresentano rotazioni pure, cioè trasformazioni che conservano non solo le distanze e gli angoli, ma anche l’orientamento dello spazio.
Quelle con determinante -1, invece, rappresentano le riflessioni, quelle che ribaltano l’orientamento.
Nota. Questo concetto è fondamentale in fisica e in geometria: per esempio, il gruppo $ SO(3) $ descrive tutte le rotazioni nello spazio tridimensionale, mentre $ SO(2) $ descrive le rotazioni nel piano.
E così via.
