La matrice identità

Una matrice identità di ordine n è una matrice quadrata diagonale con tutti gli elementi sulla diagonale principale uguali a uno e tutti gli altri elementi uguali a zero. Per questa ragione è anche detta matrice unità o matrice identica.

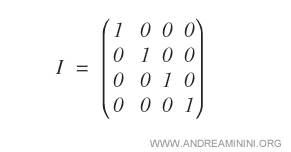
Pertanto, la matrice identità è un caso di matrice diagonale.

La matrice identità è indicata con il simbolo I_(n)=(δ_ij) dove n è la dimensione mentre gli elementi δ_ij sono detti delta di Kronecker.

Nota. La matrice identità è un caso di matrice scalare in cui tutti gli elementi della diagonale sono uguali a uno.

Le proprietà delle matrici identità

Alcune proprietà e caratteristiche delle matrici identità

• La matrice identità è l'elemento neutro della moltiplicazione riga per colonne tra matrici
  Il prodotto tra una matrice M (quadrata o rettangolare) con n colonne e la matrice identità I di ordine n è uguale alla matrice stessa M. $$ M \cdot I = M $$

  Esempio. $$ M \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

  Se la matrice è rettangolare bisogna fare attenzione perché nella moltiplicazione tra matrici il numero delle colonne della prima matrice deve essere uguale al numero di righe della seconda matrice.
  
  • Per ogni matrice A con n colonne si ha $$ AI_n=A $$

    Esempio. $$ A \cdot I_2 = A \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

  • Per ogni matrice B con n righe si ha $$ I_nB = B $$

    Esempio. $$ I_3 \cdot A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

• Le matrici identità godono della proprietà commutativa del prodotto se l'altra matrice è quadrata
  Date due matrici quadrate A e B, se almeno una delle due è una matrice unitaria è indifferente l'ordine delle matrici nella moltiplicazione ( AB = BA ) perché il risultato è sempre lo stesso.

  Nota. Le matrici identità si distinguono dalle matrici in generale che, invece, non rispettano la proprietà commutativa nella moltiplicazione tra matrici.

• Il determinante della matrice identità è sempre uguale a 1 $$ \text{det} (I) = 1 $$

E così via.