Il metodo di eliminazione di Gauss

Il metodo di eliminazione di Gauss determina l'insieme delle soluzioni possibili di un sistema lineare.

Nota. Per convenzione il metodo di Gauss si applica alle righe della matrice. Tuttavia, il metodo funziona anche se applicato alle colonne. Pertanto, in particolari esigenze pratiche si può calcolare anche utilizzando le colonne anziché le righe.

E' anche conosciuto come metodo di eliminazione di Gauss-Jordan. Pur essendo quest'ultima una variante del metodo di eliminazione di Gauss.

A cosa serve?

Il metodo di eliminazione di Gauss trasforma un sistema di equazioni lineari in una sistema a gradini.

Questo rende molto più semplice il calcolo del rango e la ricerca delle soluzioni del sistema lineare quando il sistema è composto da numerose equazioni e variabili.

Come funziona il metodo di eliminazione di Gauss

Con questo metodo si cerca una matrice equivalente che sia più facilmente analizzabile.

Cos'è una matrice equivalente? E' una matrice con i due sistemi lineari associati equivalenti. Quindi, il sistema lineare associato alla matrice equivalente M' ha le stesse soluzioni del sistema lineare associato alla matrice di origine M ma è più facile da analizzare.

Il metodo di eliminazione di Gauss-Jordan consiste nel ridurre la matrice iniziale in una matrice a gradini ( o matrice a scalini ).

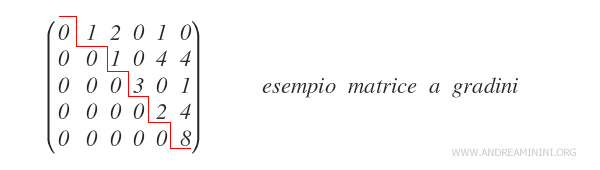
Ogni gradino della scala diverso da zero è detto pivot.

Nota. Il pivot è il primo elemento diverso da zero a partire da sinistra di una riga non nulla. E' anche detto termine direttore.

Quali sono le caratteristiche di una matrice a gradini?

Una matrice a gradini ha le seguenti caratteristiche:

1. le righe nulle si trovano in basso
   
   

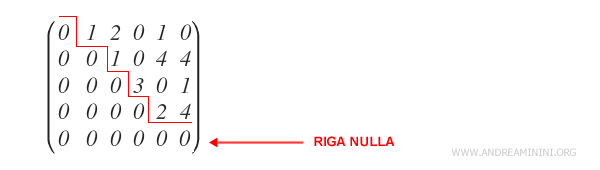
   Cos'è una riga nulla? Per riga nulla si intende una riga con tutti gli elementi uguali a zero.

2. il pivot di ogni riga non nulla si trova in una colonna a destra rispetto ai pivot delle righe precedenti.
   

Per costruire la scala della matrice equivalente si possono compiere alcune operazioni ammissibili di trasformazione dette "mosse di Gauss".

Quali sono le mosse di Gauss

Le operazioni ammissibili sulla matrice, secondo Gauss, sono le seguenti:

1. Scambio di una riga con un'altra riga
   
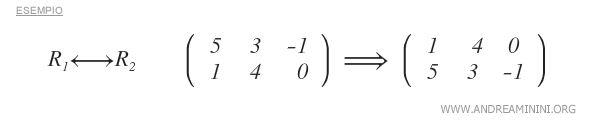
2. Moltiplicazione di una riga per un numero reale diverso da zero
   
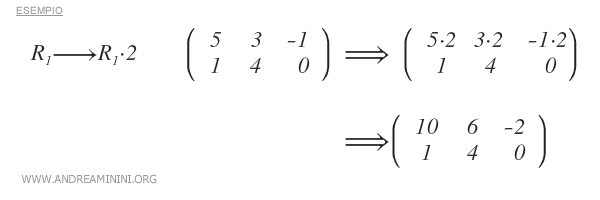
3. Somma di due righe tra loro
   

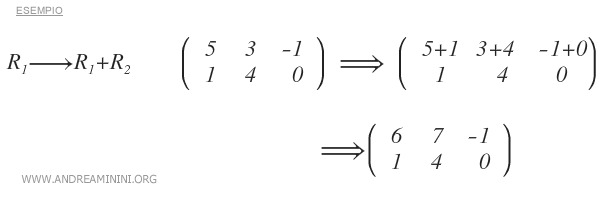
Nota. E' anche possibile unire in un'unica operazione le ultime due operazioni, ossia sommare a una riga il multiplo di un'altra riga.

L'algoritmo di Gauss

Data una matrice A con m righe e n colonne, per calcolare una matrice equivalente in forma a scalini.

Nota. Se la matrice è nulla l'algoritmo si conclude subito.

Passo 1

Individuo la prima colonna j non nulla di A a partire da sinistra.

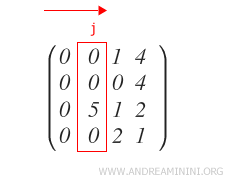
Se il primo elemento della colonna j è diverso da zero vado al passo 2.

In caso contrario, se uguale a zero, cerco la prima riga Rx che abbia il j-esimo elemento diverso da zero

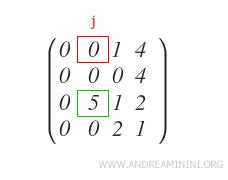
Quindi scambio la R₁ con la riga R_x e vado al passo 2.

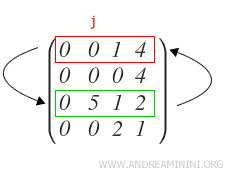
Nota. La notazione per indicare questa operazione di sostituzione è la seguente:

In questo modo ottengo il primo pivot ( p₁ ) della matrice.

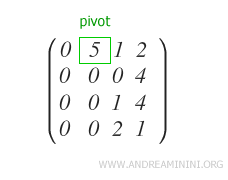
Passo 2

Verifico che gli altri elementi q_j-esimi delle righe R_i sottostanti al pivot siano tutti uguali a zero.

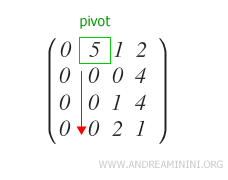
In caso contrario, se qualche elemento è diverso da zero applico la seguente sottrazione alla riga R_i.

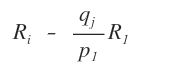
In questo modo posso annullare gli eventuali elementi diversi da zero sotto il pivot.

Una volta arrivato all'ultima riga vado al passo 3.

Passo 3

Individuo la prima colonna j-esima a destra dell'ultimo pivot che non abbia tutti zeri nelle righe sottostanti al pivot.

Se questa colonna non esiste, l'algoritmo finisce qui.

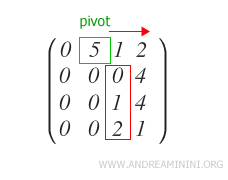
In questo caso la colonna esiste.

Il primo elemento della colonna è uno zero. Quindi, cerco la prima riga sottostante con valore diverso da zero e sostituisco le righe.

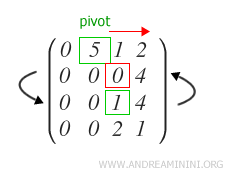
In questo modo ho trovato il secondo pivot p₂ della matrice a gradino.

Se il pivot si trova sull'ultima riga della matrice (m) l'algoritmo termina qui.

In questo caso mi trovo soltanto alla seconda riga ( R₂ ) su quattro, quindi procedo e vado al passo 4.

Passo 4

Verifico che gli altri elementi q_j-esimi delle righe R_i sottostanti all'ultimo pivot p_k siano tutti uguali a zero.

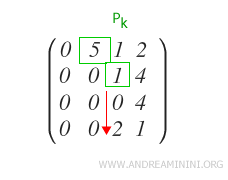
In questo caso trovo un elemento diverso da zero nella riga R_i ( i=4 ).

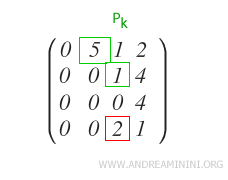
Per annullarlo devo applicare la seguente sottrazione alla riga R_i.

Applico la formula su tutti gli elementi della riga.

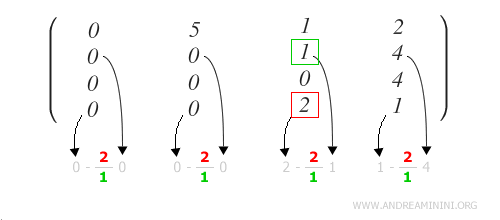
Nota. Sui primi elementi della riga è inutile applicarlo in quanto si annulla automaticamente con gli zeri della riga pivot. Per semplicità espositiva ho comunque preferito applicarlo a tutta la riga.

Una volta svolti i calcoli ottengo la seguente situazione.

Ho così ottenuto una matrice a scalini.

E così via.