Il rango della matrice
Il rango di una matrice A è il minore non nullo con ordine più grande. E' anche detto caratteristica della matrice.
Data una matrice A di tipo mxn ha rango p se esiste almeno un minore di ordine p con determinante non nullo e tutti i minori di ordine p+1, se esistono, hanno un determinante nullo.

Il rango della matrice A è un numero reale ed è indicato con il simbolo rk(A), rg(A), r(A), p(A).
Nota. Spiegato in modo più semplice, data una matrice qualsiasi il rango è l'ordine massimo dei minori con determinante non nullo.
A cosa serve il rango?
Il rango indica il numero di righe o colonne linearmente indipendenti della matrice.
Come calcolare il rango della matrice
Se la matrice A appartiene Mmxn allora il rango della matrice r(A) è compreso tra zero e il numero intero minore tra righe e colonne.
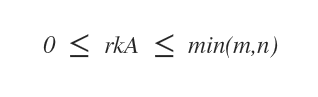
Il numero di righe/colonne linearmente indipendente non può essere superiore al numero di righe e di colonne della matrice.
Nota. Per convenzione soltanto la matrice nulla ha rango zero. Tutte le altre matrici hanno un rango maggiore o uguale a 1.
Un esempio pratico
Nel seguente esempio calcolo il rango di una matrice 3x4.

Il rango della matrice è uguale a 3.
Nota. Per calcolare il rango non occorre verificare tutti i minori di ogni ordine della radice. E' sufficiente trovare il primo minore diverso da zero nell'ordine N per passare all'ordine successivo N+1.
Il rango massimo o pieno
Se rango=min(m,n) allora si dice rango massimo o rango pieno.
Un esempio pratico

Nota. Nelle matrici quadrate di ordine n il rango potrebbe coincidere con l'ordine della matrice stessa, rg(A)=n , soltanto se il determinante della matrice è diverso da zero.
Le proprietà del rango
Il rango delle matrici ha le seguenti proprietà:
- Il rango di una matrice A è uguale al rango della matrice trasposta AT.
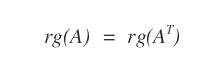
- Il rango è uguale a zero soltanto nelle matrici nulle.
- Se tutti i minori di ordine N sono nulli, allora sono nulli anche tutti gli ordini superiori a N della matrice.
Dimostrazione. Per ipotesi tutti i minori di ordine k di una matrice sono nulli, dove k è minore al valore minimo tra il numero di righe m e di colonne n ( k<min{m,n} ). Consideriamo un minore di ordine j dove k<j≤min{m,n}. Nello sviluppo di Laplace il determinante di una matrice di ordine j si riduce al calcolo dei determinanti delle sottomatrici quadrate di ordine j-1. E così via fino al calcolo dei determinanti delle sottomatrici quadrate di ordine j-1=k. Essendo nulli i minori di ordine k, si dimostra così che anche tutti i minori di ordine superiore a k sono nulli.
Altri metodi di calcolo del rango
Il rango della matrice può essere ottenuto calcolando tutti i minori della matrice.
Tuttavia, questo metodo è abbastanza lungo.
Quali sono i metodi alternativi per calcolare il rango?
Per ridurre i calcoli si possono utilizzare altri metodi più rapidi come i seguenti:
- il teorema degli orlati ( o teorema di Kronecker )
- il metodo di eliminazione di Gauss
Il rango e la rappresentazione grafica dei vettori
Dal punto di vista grafico il rango di una matrice composta da vettori riga o colonna, ci dice quanta informazione indipendente abbiamo per rappresentare graficamente i vettori nello spazio.
Ad esempio, considero questa matrice 2x3
$$ M_1 = \begin{pmatrix} 1 & 0 & 3 \\ 0 & 2 & 1 \end{pmatrix} $$
La matrice seguente ha il rango pari a 2.
$$ rk(M_1)= 2 $$
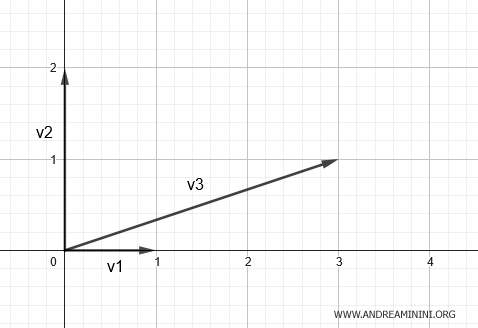
Questo vuol dire che i vettori colonna v1=(1;0), v2=(0;2), v3=(3;1) possono essere rappresentati in due direzioni indipendenti, ossia sul piano.
Faccio un altro esempio.
$$ M_2 = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \end{pmatrix} $$
Questa matrice ha il rango uguale a 1 perché una riga è multipla dell'altra. Quindi, l'informazione è la stessa.
$$ rk(M_2)= 1 $$
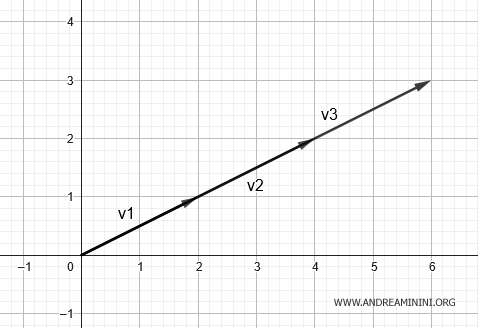
Questo significa che i vettori v1=(2;1), v2=(4;2), v3=(6;3) sono rappresentabili in uno spazio a una dimensione, ossia su una linea.
In questo caso, manca l'informazione su una delle dimensioni del piano.
Nota. In generale, se ho una matrice di n-dimensioni con n>3, pur non essendo più rappresentabile graficamente, il rango mi indica quanta informazione indipendente ho a disposizione.
Osservazioni
Alcune osservazioni utili sul calcolo del rango di una matrice
- Due matrici equivalenti per riga A e B hanno lo stesso rango $$ rk(A) = rk(B) $$ Vale sia per le matrici quadrate che rettangolari.
- Il rango è un invariante completo della trasposizione perché una qualsiasi matrice quadrata M e la sua matrice trasposta MT hanno sempre lo stesso rango $$ rk(M) = rk(M^T) $$
FAQ
- Qual è la matrice con rango uguale a zero?
L'unica matrice con rango uguale a zero è la matrice nulla. - Quando la matrice ha rango pieno?
La matrice ha rango pieno ( o rango massimo ) quando il rango è uguale al minimo tra il numero delle righe e il numero delle colonne.
