Il complemento algebrico o cofattore
Il complemento algebrico è il minore complementare della sottomatrice A(ij) moltiplicato per uno scalare (-1)i+j. E' anche detto cofattore aij.
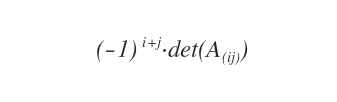
Come calcolare il cofattore
Data una matrice A, calcolo il minore complementare dell'elemento aij,
Cos'è il minore complementare? Il minore complementare dell'elemento aij è il determinante della sottomatrice complementare ottenuta eliminando la riga i e la colonna j dalla matrice.

Poi moltiplico il minore complementare per (-1)ij
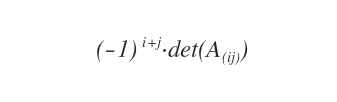
Ho così calcolato il cofattore di aij.
Il segno del cofattore cambia a seconda della posizione dell'elemento aij nella matrice.
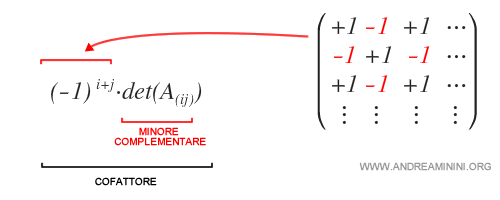
Quindi, in alcuni casi il cofattore coincide con il minore complementare mentre in altri ha segno opposto.
Un esempio pratico
Ho una matrice quadrata A di ordine 3.
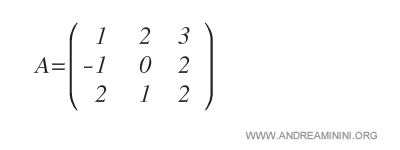
Voglio calcolare il cofattore di a11.
Estraggo la sottomatrice complementare di aij
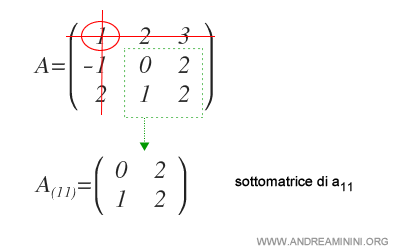
Poi calcolo il determinante della sottomatrice A(11) ossia il minore complementare di a11
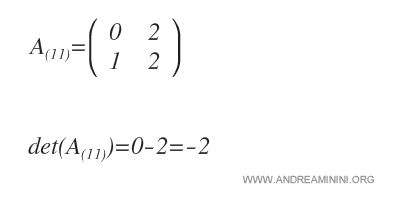
Infine, moltiplico il minore complementare per (-1)i+j ossia per (-1)2 poiché le coordinate dell'elemento sono i=1 e j=1.
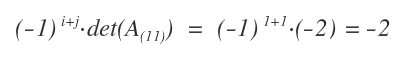
Quindi il cofattore di a11 è -2.
In questo caso il cofattore coincide con il minore complementare di a11. Tuttavia, non è sempre così perché dipende dalla posizione dell'elemento.
Nota. Se avessi calcolato il cofattore di a12, invece, avrebbe avuto il segno opposto perché (-1)1+2=-1. Il minore complementare di a12 è -6 mentre il cofattore di a12 è 6.

Allo stesso modo posso calcolare tutti gli altri cofattori della matrice.
