La sottomatrice
Una sottomatrice è una matrice ottenuta selezionando soltanto alcune righe e colonne di una matrice di riferimento, senza modificarne l'ordine.
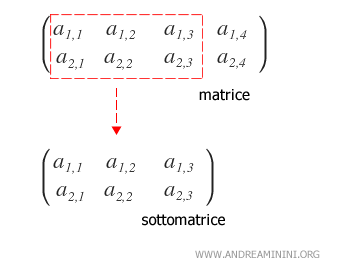
La definizione di sottomatrice. Siano I={1,...,m) e J={1,...,n) sottoinsiemi di Z, e sia A=(aij) una matrice mxn in cui i∈I e j∈. Dati due sottoinsiemi H e K rispettivamente di I e J la sottomatrice di A è una matrice AHK=(aij) con i∈H e j∈K.
Un esempio pratico di sottomatrice
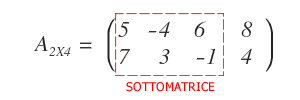
La seguente matrice A2X4 è composta da due righe ( m=2 ) e quattro colonne ( n=4 ).
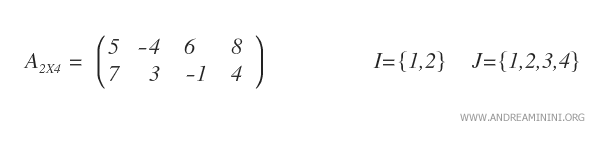
Seleziono due sottoinsiemi H e K rispettivamente di I e J.
In questo modo ottengo una sottomatrice AHK.
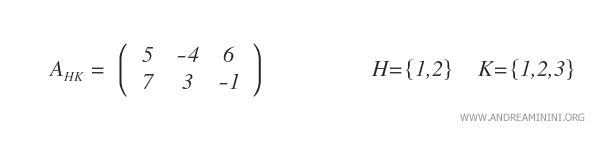
Nota. In questo caso ho selezionato le prime tre colonne eliminando l'ultima.
Tuttavia, non necessariamente le righe e le colonne devono essere contigue.
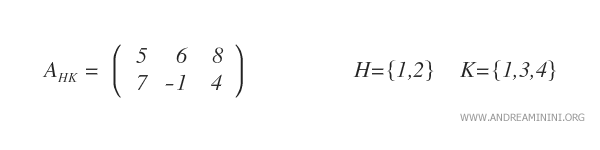
Nota. In questo caso ho costruito la sottomatrice selezionando la prima, la terza e la quarta colonna. E così via.
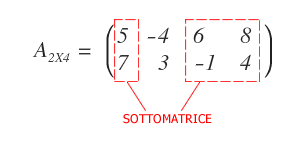
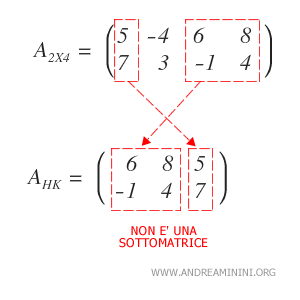
Ciò che conta è che la sottomatrice rispetti sempre l'ordine delle righe e delle colonne della matrice originaria.
Esempio. Se modificassi l'ordine delle colonne non sarebbe più una sottomatrice anche se gli elementi selezionati sono sempre gli stessi. Questa non è una sottomatrice.