L'operazione pivot

L'operazione pivot è un'operazione del calcolo matriciale in grado di trasformare una matrice m x n sostituendo la k-esima colonna della matrice con la h-esima colonna della matrice identità di dimensioni m.

Per eseguire un'operazione pivot devo selezionare un elemento della matrice non nullo, detto elemento pivot.

Se un elemento è nullo, non è possibile selezionarlo come elemento pivot.

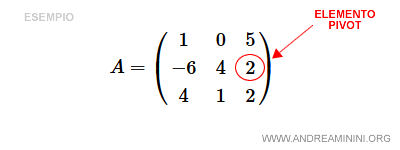
L'operazione pivot si realizza con due operazioni in sequenza:

1. Divido la riga h dell'elemento pivot (detta riga pivot) per l'elemento pivot a_hk. $$ \bar{a}_{h} = \frac{a_{hi}}{a_{hk}} $$ Questa operazione rende l'elemento pivot uguale a 1.
2. A ogni altra riga j della matrice sottraggo la nuova riga h dell'elemento pivot a_hk moltiplicata per l'elemento corrispondente alla colonna pivot a_jk. $$ \bar{a}_{j} = a_{j} - a_{jk} \cdot \bar{a}_{h} $$

Questa operazione annulla tutti gli elementi della colonna dell'elemento pivot.

Un esempio pratico

Ho la matrice

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

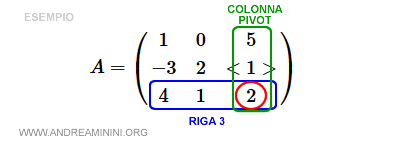
Seleziono come elemento pivot l'elemento a₂₃ ossia il terzo elemento (k=3) sulla seconda riga (h=2).

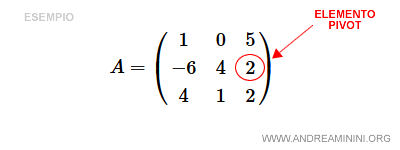
Quindi la colonna pivot è la terza (k=3) mentre la riga pivot è la seconda (h=2).

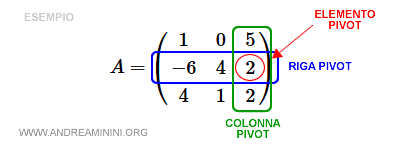
Per semplicità indico l'elemento tra i simboli <>.

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & <2> \\ 4 & 1 & 2 \end{pmatrix} $$

Divido tutti i termini della riga pivot (h=2) per l'elemento pivot a₂₃=2

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ \frac{-6}{2} & \frac{4}{2} & <\frac{2}{2}> \\ 4 & 1 & 2 \end{pmatrix} $$

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -3 & 2 & <1> \\ 4 & 1 & 2 \end{pmatrix} $$

La seconda riga a₂ è stata modificata e l'elemento pivot è diventato uguale a 1.

Poi sottraggo a ogni altra riga della matrice la nuova riga a₂ moltiplicata per l'elemento corrispondente alla colonna pivot (k=3).

Riga 1

La prima riga è [1, 0, 5] e l'elemento della riga corrispondente alla colonna pivot (k=3) è 5.

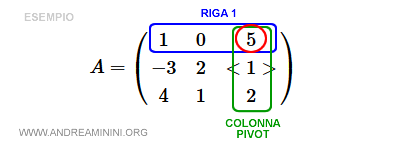
$$ a_1 = [ 1 \:\: 0 \:\: 5] - 5 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_1 = [ 1 \:\: 0 \:\: 5] - [-15 \:\: 10 \:\: 5] $$

$$ a_1 = [ 16 \:\: -10 \:\: 0] $$

Riga 2

La riga 2 è la riga pivot e non va più modificata.

E' già stata aggiornata nella prima fase dell'operazione pivot.

Riga 3

La seconda riga è [4, 1, 2] e l'elemento della riga corrispondente alla colonna pivot (k=3) è 2.

$$ a_1 = [ 4 \:\: 1 \:\: 2] - 2 \cdot [ -3 \:\: 2 \:\: 1] $$

$$ a_1 = [ 4 \:\: 1 \:\: 2] - [-6 \:\: 4 \:\: 2] $$

$$ a_1 = [ 10 \: -3 \: 0] $$

Ho ottenuto i nuovi valori della prima e della terza riga.

Il risultato finale

Dopo l'operazione pivot sull'elemento a₂₃ ottengo la seguente matrice

$$ A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

L'elemento pivot è diventato pari a 1 mentre tutti gli altri elementi della colonna pivot sono diventati nulli.

Un metodo alternativo

C'è anche un altro metodo alternativo per eseguire l'operazione pivot basato sulla matrice identità m x m.

Data una matrice M di dimensioni m x n con elemento pivot a_(h,k)

1. Scrivo una matrice identità Q di dimensioni m x m
2. Sostituisco la h-esima colonna della matrice Q con la k-esima colonna della matrice M
3. Nella matrice Q sostituisco l'elemento pivot a(h,k) con il suo reciproco.
4. Moltiplico tutti gli altri elementi della colonna pivot nella matrice Q per il reciproco dell'elemento pivot a_(h,k) cambiato di segno.
5. Moltiplico la matrice Q per la matrice M $$ M' = Q \cdot M $$
6. Il prodotto è la matrice M' dopo l'operazione pivot.

Un esempio pratico

Riprendo la matrice A dell'esempio precedente.

La matrice ha m=3 righe e n=3 colonne. L'elemento pivot è a_2,3=2

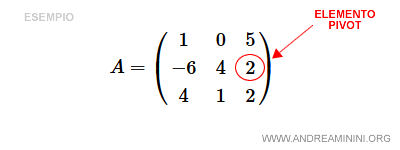
Scrivo una matrice identità Q di dimensioni m x m ossia 3 x 3

$$ Q = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Sostituisco la colonna h=2 della matrice identità Q con la colonna k=3 della matrice A.

Per ricordarmelo indico l'elemento pivot tra i simboli < >.

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & <2> & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Sostituisco l'elemento pivot nella matrice Q con il suo reciproco.

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & \frac{1}{<2>} & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Moltiplico gli altri elementi della colonna h=2 della matrice Q con il reciproco dell'elemento pivot cambiato di segno.

$$ Q = \begin{pmatrix} 1 & 5 \cdot ( - \frac{1}{2} ) & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 2 \cdot ( - \frac{1}{2} ) & 1 \end{pmatrix} $$

$$ Q = \begin{pmatrix} 1 & - \frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} $$

Poi moltiplico la matrice Q per la matrice A

$$ Q \cdot A = \begin{pmatrix} 1 & - \frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

$$ Q \cdot A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

Il risultato finale è lo stesso.

E così via.