La matrice

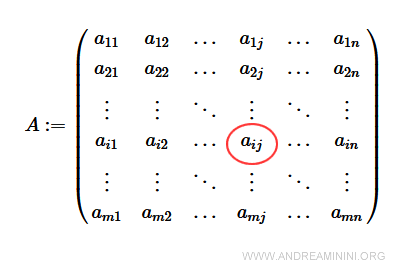
Una matrice è una tabella ordinata di elementi a_i,j. Dove a_i,j sono numeri detti elementi (o coefficienti) e gli indici i,j in pedice agli elementi sono dei numeri interi positivi che indicano per convenzione prima il numero di riga (i) e poi il numero di colonna (j).

Se gli elementi sono numeri reali, la matrice è detta matrice a coefficienti reali.

Un generico elemento di posto (i,j) si trova nella i-esima riga e j-esima colonna.

Gli indici degli elementi possono essere indicati con la virgola (a_m,n) o senza la virgola (a_mn) tra gli indici.

Nota. La notazione con la virgola evita le ambiguità quando gli indici superano la decina.

Altre notazioni sintetiche per indicare la matrice sono A_(m,n) , A_mxn o A=(a_mn).

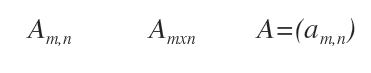
Il numero complessivo delle righe e delle colonne ( mxn ) è detto dimensione della matrice.

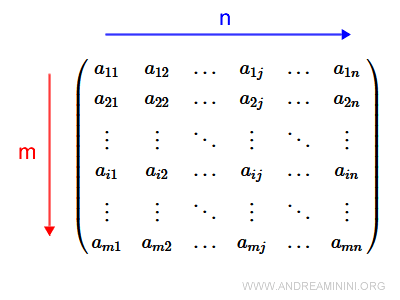
Quindi m e n sono le dimensioni di una generica matrice di tipo (m,n).

Se il numero di righe è uguale al numero delle colonne (m=n) la matrice è detta matrice quadrata.

A cosa serve la matrice? Le matrici sono oggetti matematici usate soprattutto nell'algebra lineare per rappresentare e risolvere i sistemi lineari di m equazioni e n variabili.

Un esempio di matrice

Questa è una matrice di tipo (2,3)

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

Gli elementi della matrice sono

$$ a_{11}=3 \\ a_{12} = 1 \\ a_{13} = 6 \\ a_{21}=0 \\ a_{22} = 4 \\ a_{23} = -1 $$

Dove gli elementi a₁₁, a₁₂, a₁₃ sono i coefficienti della prima riga della matrice.

Gli elementi a₂₁, a₂₂, a₂₃ sono i coefficienti della seconda riga della matrice.

Attenzione. L'ordine degli elementi è fondamentale in una matrice. Una diversa disposizione degli elementi genera una matrice diversa. Ad esempio, definisco una matrice B invertendo le righe della matrice A. $$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$ $$ B : = \begin{pmatrix} 0 & 4 & -1 \\ 3 & 1 & 6 \end{pmatrix} $$ Le matrici A e B hanno gli stessi elementi ma sono matrici diverse. E' importante ricordarlo.

Gli insiemi delle matrici

L'insieme di tutte le matrici di dimensione mxn con elementi reali ( matrici reali ) è indicato con la notazione M_m,n(R) oppure M(m,n,R).

$$ M_{m,n}(R) = M(m,n,R) $$

L'insieme delle matrici quadrate si indica in questo modo

$$ M_{n,n}(R) = M(n,n,R) $$

Esempio

La matrice A è una matrice composta da 2 righe e 3 colonne.

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

Pertanto, la matrice A appartiene all'insieme delle matrici di tipo 2x3.

$$ A \in M(2,3,R) $$

Nota. La matrice A appartiene all'insieme delle matrici di tipo 2x3 a coefficienti reali ossia M(2,3,R). Pertanto, i suoi elementi non sono soltanto numeri interi bensì numeri reali (R). Se voglio definire una matrice composta solo di numeri interi devo scrivere M(2,3,Z) dove Z è l'insieme dei numeri interi. L'insieme delle matrici M(2,3,Z) è un sottoinsieme di M(2,3,R) poiché, a parità di dimensioni delle matrici, i numeri interi sono un sottoinsieme dei numeri reali Z⊂R .

Tipi di matrici

In base alla dimensione, al numero di righe e di colonne, posso distinguere le seguenti tipologie di matrici:

• La matrice rettangolare. Sono matrici con più righe (m>1) e colonne (n>0) in cui il numero di righe non eguaglia il numero delle colonne (m≠n). Da questa caratteristica deriva la sua forma rettangolare.
  
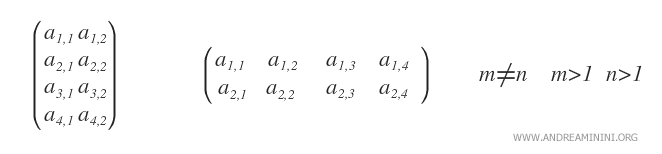
• La matrice quadrata. Sono matrici con lo stesso numero di righe e colonne ( m=n ). Da questa caratteristica deriva la sua forma quadrata.
  
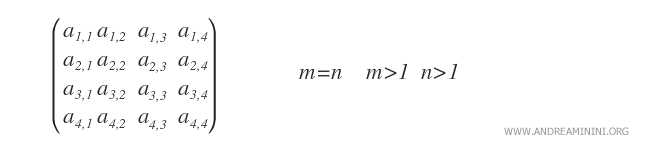
• La matrice riga. Sono matrici 1xn con una sola riga ( m=1 ).
  
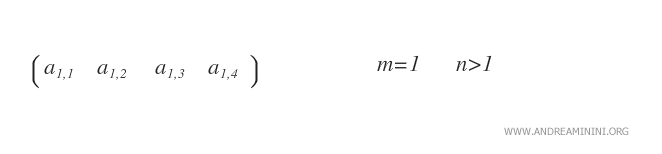
• La matrice colonna. Sono matrici mx1 con una sola colonna ( n=1 ).
  
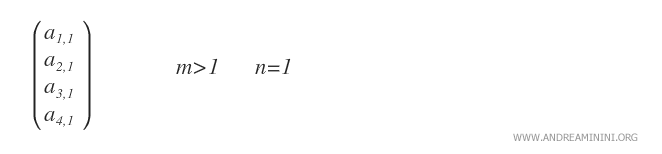
• La matrice nulla. Sono matrici senza nessun elemento, senza righe ( m=0) e senza colonne ( n=0 ).

Come rappresentare un sistema lineare con una matrice

Dato un sistema lineare A composto da m equazioni e n variabili

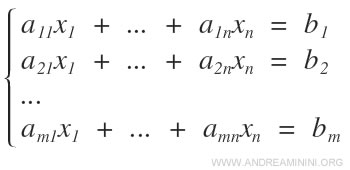
il sistema lineare è sempre associabile a due matrici:

1. La matrice dei coefficienti ( o matrice incompleta ) è una matrice di m righe e n colonne, in cui gli elementi sono i coefficienti amn delle equazioni nel sistema lineare.
   
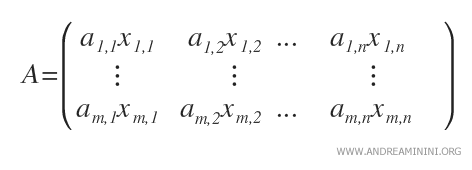
2. La matrice completa ( o matrice orlata ) è una matrice di m righe e n+1 colonne, composta sia dai coefficienti a_mn che dai termini noti b_m del sistema lineare.
   

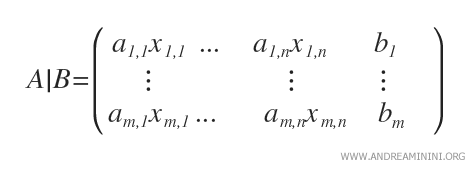
   Nota. In pratica la matrice completa è la matrice dei coefficienti con l'aggiunta della colonna dei termini noti.

Un esempio pratico

Questo sistema lineare è formato da due equazioni e tre variabili.

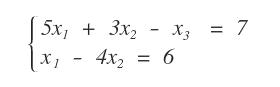
La matrice dei coefficienti A è la seguente:

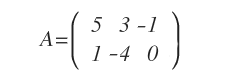
Nota. Nella seconda equazione del sistema (x₁-4x₂=6) non c'è la variabile x₃. In questi casi si mette il valore zero nell'elemento corrispondente della matrice.

La matrice completa A|B del sistema è, invece, la seguente:

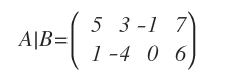
Nota. Alla matrice dei coefficienti ho aggiunto semplicemente la colonna dei termini noti.

E così via.