Le matrici simili
Due matrici A e B di ordine n si dicono simili se esiste una matrice invertibile M tale che:
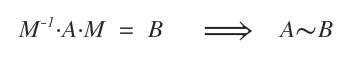
In tale caso le due matrici si indicano con l'operatore della similitudine ∼ ( tilde )
La similitudine è una relazione di equivalenza nell'insieme di tutte le matrici di ordine n.
Le proprietà delle matrici simili
- Ogni matrice è simile a se stessa
- Se la matrice A è simile a B, la matrice B è simile a A
- Se la matrice A è simile a B e la matrice B è simile a C, allora la matrice A è simile C.
- Due matrici simili condividono gli stessi autovalori e hanno lo stesso determinante, rango e traccia.
- Due matrici simili sono un endomorfismo rispetto alle basi diverse B1 e B2 di uno spazio vettoriale V.
- Due matrici simili hanno lo stesso polinomio caratteristico.
Un esempio pratico di matrici inverse
Queste due matrici A e B
$$ A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} $$
$$ B = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
Sono simili perché esiste una matrice invertibile M
$$ M = \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} $$
$$ M^{-1} = \begin{pmatrix} 1/6 & -1/3 & 1/6 \\ 1/3 & 1/3 & 1/3 \\ 1/2 & 0 & -1/2 \end{pmatrix} $$
Tale che
$$ M^{-1}AM = B $$
Infatti
$$ \begin{pmatrix} 1/6 & -1/3 & 1/6 \\ 1/3 & 1/3 & 1/3 \\ 1/2 & 0 & -1/2 \end{pmatrix} \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
E così via
