Le matrici invertibili e inverse

Una matrice quadrata A di ordine è n invertibile se esiste una matrice inversa A^-1 dello stesso ordine, tale che i prodotti AA^-1 e A^-1A sono uguali a una matrice unitaria I ( matrice identità ).

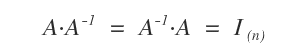
Le matrici inverse sono indicate con il simbolo -1 in apice.

Nota. Il concetto di matrice inversa è molto simile al reciproco dei numeri naturali. Tutti i numeri reali, a parte lo zero, hanno sempre un reciproco tale che $$ a \cdot b = a \cdot \frac{1}{a} = 1 \ \ \ \ \ a,b \in R $$ Allo stesso modo le matrici invertibili M hanno una matrice inversa M^-1 tale che il loro prodotto restituisce una matrice identità $$ M \cdot M^{-1} = I $$ La matrice identità corrisponde al numero 1 dei numeri reali perché il prodotto di qualsiasi matrice M per la matrice identità I è uguale alla matrice stessa. $$ M \cdot I = M $$

Non tutte le matrici sono invertibili. Esistono molte matrici che non hanno una matrice inversa.

L'insieme delle matrici reali invertibili di ordine n è indicato con il termine GL_n(R) o GL(n,R).

$$ GL(n,R) $$

E' anche detto gruppo lineare di ordine n con coefficienti reali.

Nota. L'insieme GL_n(R) è un insieme chiuso rispetto al prodotto tra matrici. La matrice identità I è un elemento dell'insieme GL_n(R).

Un esempio pratico di matrice inversa

La seguente matrice è una matrice invertibile

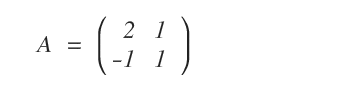
perché moltiplicando A per la sua matrice inversa A^-1 si ottiene come risultato una matrice identità I₍₂₎ dello stesso ordine.

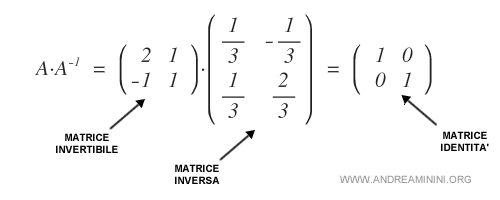
Come calcolare la matrice inversa

Per calcolare la matrice inversa di una matrice invertibile posso seguire due strade:

Nota. Il secondo metodo è quello preferibile perché riduce i calcoli. In ogni caso, il primo metodo è utile per capire l'equivalenza teorica tra matrici e sistemi lineari.

Metodo 1

Data una matrice A, voglio capire se è una matrice invertibile ed eventualmente qual è la sua matrice inversa A^-1.

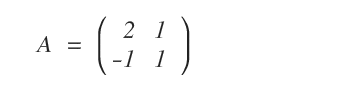
Se A è una matrice invertibile allora vale l'equazione A*A^-1= I

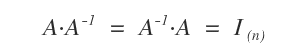
Quindi, moltiplico A per una matrice B dello stesso ordine composta da variabili incognite.

Poi eguaglio il prodotto a una matrice identità I.

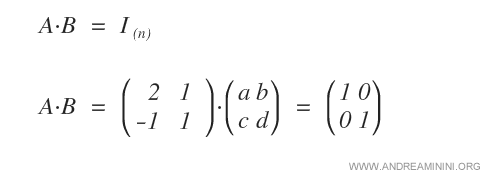
Svolgo la moltiplicazione riga per colonna delle due matrici.

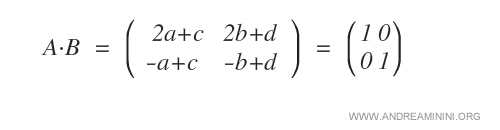
A questo punto scrivo il sistema lineare equivalente all'uguaglianza delle due matrici

Se il sistema lineare ha una soluzione, allora la matrice è invertibile.

In questo caso il sistema lineare ha una soluzione.

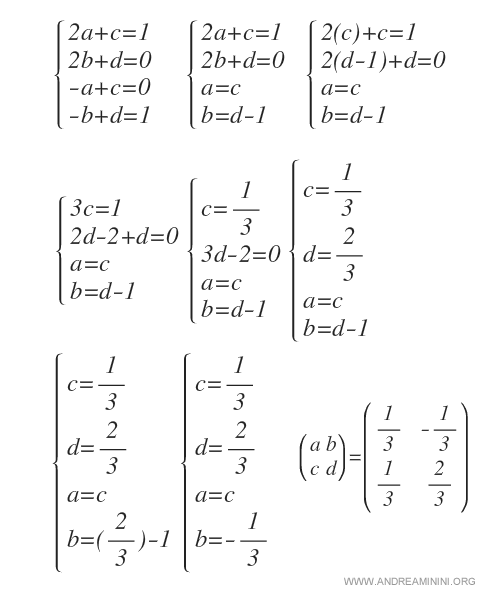Dimostrazione

Dalla risoluzione del sistema ottengo i valori delle incognite a, b, c, d, ossia gli elementi della matrice inversa.

In questo modo ho verificato che A è una matrice invertibile e ho trovato la matrice inversa.

Attenzione. Questo metodo è un po' lungo e diventa molto complesso se la matrice ha un ordine superiore a 2. E' però utile per capire. Per calcolare la matrice inversa è preferibile usare il secondo metodo.

Metodo 2

Se la matrice quadrata è di ordine 1 ossia è composta da un solo elemento non nullo A={a₁₁} allora la sua matrice inversa è $$ A^{-1}=(a_{11}^{-1}) $$ Se la matrice quadrata è di ordine superiore a 1 allora la matrice inversa è $$ A^{-1} = \frac{1}{det(A)} \cdot cof(A)^T $$

Data una matrice quadrata A, cerco di capire se è una matrice invertibile e qual è la sua matrice inversa A^-1.

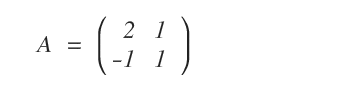
Secondo il teorema di esistenza della matrice inversa, una matrice è invertibile se e soltanto se il suo determinante è diverso da zero.

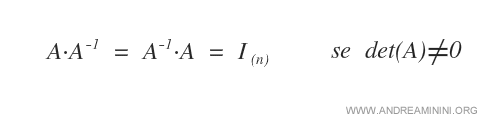
In questo caso, il determinante Δ della matrice A è diverso da zero.

Quindi A è una matrice invertibile.

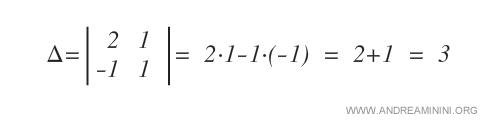
Nota. Se il determinante di A fosse stato uguale a zero avrei potuto affermare con certezza che la matrice non è invertibile e concludere qui i calcoli.

Ora bisogna capire qual è la matrice inversa.

Per farlo c'è un teorema, sia A una matrice quadrata invertibile, tale che det(A)≠0, allora la matrice inversa A^-1 è uguale al prodotto tra l'inverso del determinante di A e la trasposta dei cofattori.

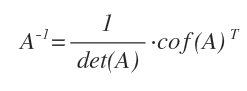
Nota. La dimostrazione del teorema è un po' lunga.

Il determinante det(A) già lo conosco.

Quindi calcolo la matrice dei cofattori ( o matrice dei complementi algebrici ) di A.

La matrice dei cofattori è indicata con il simbolo cof(A).

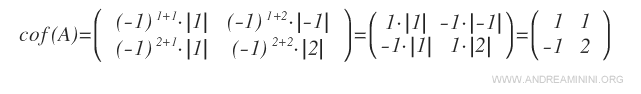
Nota. Il complemento algebrico di un elemento a_ij della matrice A è determinato dalla seguente formula.

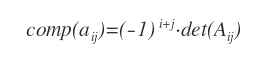
Poi calcolo la matrice trasposta della matrice dei cofattori.

La trasposta dei cofattori è detta matrice aggiunta di A ed è indicata con il simbolo A*.

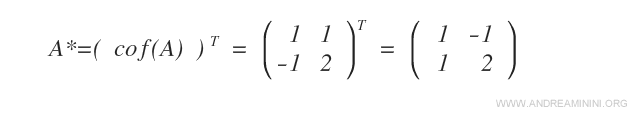
Moltiplicando la matrice aggiunta per l'inverso del determinante di A, ottengo la matrice inversa di A.

Ho così trovato la matrice inversa di A.

Per fare una verifica basta sostituire la matrice inversa appena trovata all'equazione AA^-1=I.

Il prodotto AA^-1 è una matrice identità.

Nota. C'è anche un terzo metodo per calcolare la matrice inversa, tramite l'algoritmo di eliminazione di Gauss-Jordan.

Le caratteristiche delle matrici inverse e invertibili

Le matrici inverse e invertibili hanno le seguenti caratteristiche:

• Solo le matrici quadrate possono essere invertibili. Se la matrice inversa esiste allora è unica.
• La matrice inversa non è uguale al reciproco degli elementi. Se esiste, la matrice inversa può essere composta da qualsiasi valore, con elementi diversi o uguali alla matrice invertibile. In alcuni casi la matrice inversa potrebbe essere anche uguale alla matrice invertibile.

  Esempio. Le matrici identità sono sempre invertibili per se stesse, ossia la matrice inversa di I_(n) è uguale a I_(n).
  

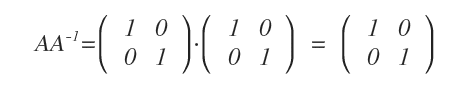
• Se la matrice A è invertibile, allora anche la matrice inversa A^-1 è invertibile.
  L'inversa della matrice inversa (A^-1)^-1 è uguale alla matrice A.
  
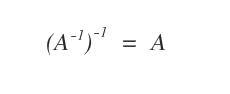
• Il determinante della matrice inversa A^-1 è uguale al reciproco del determinante della matrice invertibile A $$ det(A^{-1}) = \frac{1}{det(A)} $$

  Dimostrazione. Per il teorema di Binet il determinante di una matrice prodotto A·B è uguale al prodotto dei determinanti delle matrici det(A)·det(B) $$ det(A \cdot B) = det(A) \cdot det(B) $$ Quindi, il determinante del prodotto di una matrice invertibile per la matrice inversa è uguale al prodotto dei determinanti $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) $$ Sapendo che il prodotto di una matrice invertibile A per la matrice inversa A^-1 è il la matrice identica A·A^-1=I ne deduco che anche il determinante è lo stesso $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) = det(I) $$ Il determinante della matrice identica è sempre uguale a 1. $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) = det(I) = 1 $$ Quindi anche il determinante della matrice invertibile per il determinante della matrice inversa è sempre uguale a 1. $$ det(A) \cdot det(A^{-1}) = 1 $$ Con un semplice passaggio algebrico ottengo quello che volevo dimostrare $$ det(A^{-1}) = 1 \cdot \frac{1}{det(A} $$ $$ det(A^{-1}) = \frac{1}{det(A)} $$ Il determinante della matrice inversa A^-1 è uguale al reciproco del determinante della matrice invertibile A.

• Se la matrice A è invertibile, allora anche la matrice trasposta A^T è invertibile.
  La matrice inversa della matrice trasposta (A^T)^-1 è uguale alla trasposta della matrice inversa (A^-1)^T.
  

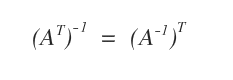
  Dimostrazione.
  

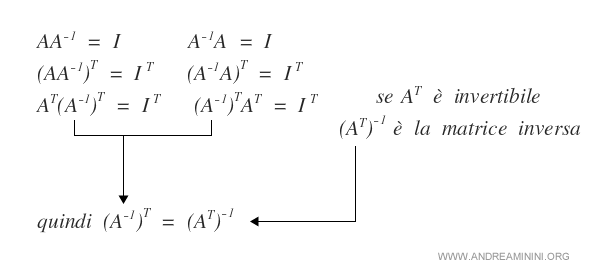
• Se le matrici A e B sono invertibili, allora anche il prodotto AB è invertibile.
  La matrice inversa del prodotto delle matrici (AB)^-1 è uguale al prodotto delle matrici inverse B^-1A^-1.
  

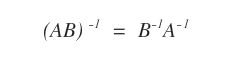
  Dimostrazione. Sapendo che il prodotto di una matrice invertibile per la sua inversa è uguale alla matrice identica. $$ (AB) \cdot (AB)^{-1} = I $$ Se (AB)^-1=B^-1A^-1 allora vale anche la seguente $$ (AB) \cdot (B^{-1}A^{-1}) = I $$ Per dimostrarlo eseguo i calcoli. $$ (AB) \cdot (B^{-1}A^{-1}) $$ Per la proprietà associativa $$ (AB) \cdot (B^{-1}A^{-1}) = A \cdot (B \cdot B^{-1}) \cdot A^{-1} $$ Sapendo che BB^-1=I $$ (AB) \cdot (B^{-1}A^{-1}) = A \cdot (B \cdot B^{-1}) \cdot A^{-1} = AIA^{-1}$$ Poiché AI=A $$ (AB) \cdot (B^{-1}A^{-1}) = A \cdot (B \cdot B^{-1}) \cdot A^{-1} = AIA^{-1} = AA^{-1} $$ Sapendo che AA^-1=I $$ (AB) \cdot (B^{-1}A^{-1}) = A \cdot (B \cdot B^{-1}) \cdot A^{-1} = AIA^{-1} = AA^{-1} = I $$ Questo dimostra che scrivere (AB)^-1 o B^-1A^-1 è la stessa cosa.
  

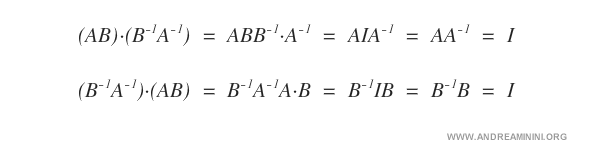
• Se la matrice ha il determinante nullo, allora non è invertibile. La matrice A è invertibile se e soltanto se la matrice A è non singolare. Una matrice è non singolare se il suo determinante è diverso da zero.

  Dimostrazione. Il determinante della matrice identità è uguale a 1 $$ det(I) = 1 $$ Poiché AB=I allora $$ det(AB)=det(I)=1 $$ Per la proprietà del determinante det(AB)=det(A)det(B) anche conosciuta come teorema di Binet $$ det(A) \cdot det(B) =det(I)=1 $$ Se il determinate di A o di B fosse nullo, anche il prodotto dei determinanti det(A)det(B)=0. $$ 0 \cdot det(B) = detA) \cdot 0 = 0 \ne det(I)=1 $$ Quindi, se det(A)=0 o det(B)=0 non può verificarsi l'uguaglianza det(A)det(B)=det(I)=1.

  Corollario. Pertanto, avendo il determinante diverso da zero, una matrice è invertibile soltanto se ha il rango massimo.

• Se la matrice inversa esiste allora è unica. Se una matrice A è invertibile allora esiste una matrice inversa A^-1 tale che AA^-1=I e la matrice inversa è unica.
  

  Dimostrazione. Considero tre matrici A,B,C tali che $$ AB=BA=I $$ $$ AC=CA=I $$ Per la proprietà associativa $$ CAB = (CA)B = C(AB) $$ Sapendo che CA=I e AB=I $$ CAB = (I)B = C(I) $$ Il prodotto di una qualsiasi matrice per la matrice identità I è la matrice stessa. Quindi IB=B e CI=C. $$ CAB = B = C $$ Poiché CAB=B e CAB=C ne consegue che B=C=CAB. Pertanto, B = C. La matrice inversa di A è unica. $$ A^{-1} = B=C $$