Esagono

L'esagono è una figura geometrica chiusa e poligonale con sei lati e sei angoli.

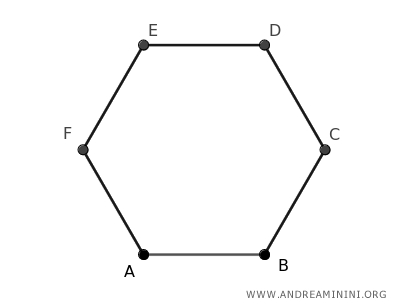
Se i lati e gli angoli di un esagono sono congruenti, si parla più propriamente di esagono regolare.

Ogni angolo interno dell'esagono regolare ha un'ampiezza di 120°.

Esistono anche esagoni irregolari in cui i lati hanno lunghezze diverse e le ampiezze degli angoli non sono congruenti.

Nel resto di questi appunti utilizzerò il termine "esagono" per intendere gli esagono regolari.

Le formule

Le formule principali da tenere a mente per il calcolo del perimetro (P) e dell'area (A) dell'esagono sono le seguenti:

• Perimetro
  Il perimetro dell'esagono regolare è uguale a sei volte il lato (l)  $$ P = 6 \cdot l $$
• Area
  L'area di un esagono regolare si può calcolare conoscendo l'apotema (a)  $$ A = \frac{P \cdot a}{2} \ \ \text{oppure} \ \ A = 2.598 \cdot l^2 $$ Dove $ l $ è la lunghezza di un lato, mentre $ a $ è l'apotema dell'esagono. $$ a = 0.866 \cdot l $$
• Lato
  Il lato di un esagono regolare è congruente con il raggio del cerchio circoscritto (dimostrazione) $$ l=r $$ Il lato dell'esagono regolare può essere calcolato anche conoscendo il raggio (r) del cerchio inscritto (dimostrazione) $$ l = \frac{2\sqrt{3}}{ 3 } \cdot r $$ In alternativa, conoscendo l'apotema (a) dell'esagono che coincide con il raggio del cerchio inscritto (r=a) $$ l = \frac{2\sqrt{3}}{ 3 }  \cdot a$$

Il perimetro

Il perimetro di un esagono si calcola semplicemente moltiplicando la lunghezza del lato per sei.

$$ P = 6 \cdot l $$

Spesso per indicare il perimetro si utilizza anche il simbolo "2p" con la lettera "p" minuscola.

$$ 2p = 6 \cdot l $$

Questo deriva dal fatto che la lettera minuscola "p" è usata per indicare il semiperimetro di un poligono.

$$ p = \frac{P}{2} $$

La lettera maiuscola "P" è, invece, utilizzata per indicare il perimetro. Quindi, P=2p

Esempio. Considero un esagono regolare con un lato di lunghezza l=2.

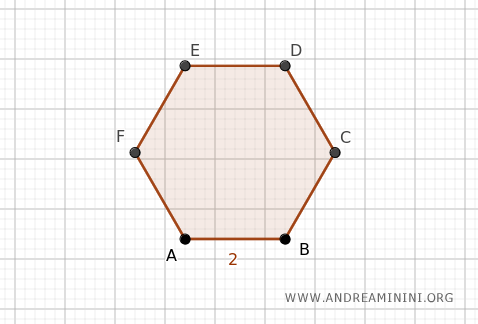
Poiché un esagono ha n=6 lati, il suo perimetro è P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Pertanto, il suo semiperimetro è semplicemente la metà del perimetro ossia p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$

L'apotema

L'apotema (a) di un esagono è il raggio della circonferenza inscritta nell'esagono.

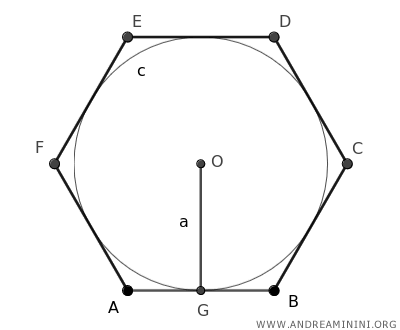
Si ottiene tracciando un segmento OG che misura la distanza minima tra il centro O e un lato qualsiasi del poligono. ,

Dal punto di vista geometrico l'apotema è il segmento perpendicolare al lato dell'esagono che ha per estremi il centro e il lato stesso dell'esagono.

La formula per calcolare l'apotema a partire dal lato "l" dell'esagono è la seguente

$$ a = l \cdot f_1 $$

Dove f₁ è uno dei due numeri fissi dell'esagono, è un valore costante pari a f₁=0.866 

Cosa sono i numeri fissi? In un esagono regolare il rapporto tra l'apotema "a" e il lato "l" è un valore costante pari a 0.866 $$ f_1 = \frac{ \sqrt{3} }{2} = 0.866 $$ Si chiama "numero fisso" perché è sempre costante al variare delle dimensioni dell'esagono.

A cosa serve?

L'apotema è molto utile per svolgere diversi calcoli geometrici. Ad esempio, mi permette di calcolare l'area dell'esagono.

L'area dell'esagono

L'area dell'esagono regolare si ottiene moltiplicando il semiperimetro (p) per l'apotema (a).

$$ A = p \cdot a $$

Dove "p" minuscola indica il semiperimetro mentre P=2p maiuscola è il perimetro dell'esagono. Quindi, il semiperimetro è p=P/2

Esempio. Un esagono regolare ha un lato lungo l=2.

Quindi, avendo n=6 lati, il suo perimetro è P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Di conseguenza, il suo semiperimetro è p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$ Calcolo l'apotema dell'esagono $$ a = 0.866 \cdot l = 0.866 \cdot 2 = 1.732 $$ Infine, calcolo l'area dell'esagono sapendo che p=6 e a=1.732 $$ A = p \cdot a = 6 \cdot 1.732 = 10.392 $$ L'area dell'esagono è 10.392.

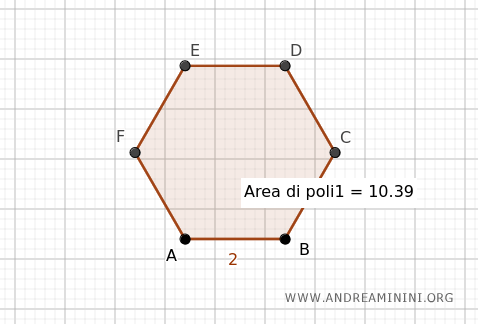
Metodo alternativo per il calcolo dell'area

L'area dell'esagono può essere calcola usando i numeri fissi dell'esagono.

$$ A = l^2 \cdot f_2 $$

Dove "l" è la lunghezza di un lato mentre f₂ è un numero fisso dell'esagono f₂=2.598.

Esempio. Considero l'esagono regolare dell'esempio precedente che ha un lato lungo l=2.

In questo caso per trovare l'area calcolo il prodotto tra il quadrato del lato per il numero fisso f₂=2.598 $$ A = l^2 \cdot f_2 = 2^2 \cdot 2.598 = 4 \cdot 2.598 = 10.392 $$ L'area dell'esagono è 10.392. E' lo stesso risultato che ho ottenuto nell'esempio precedente.

I numeri fissi dell'esagono

I numeri fissi dell'esagono sono f₁=0.866 e f₂=2.598 $$ f_1 = \frac{a}{l} = 0.866 $$ $$ f_2 = 2.598 $$ Sono molto utili nel calcolo dell'apotema e dell'area dell'esagono

Tra i due numeri fissi f₁ e f₂ c'è una relazione.

Sapendo che l'area di un esagono è il prodotto tra il semiperimetro (p) e l'apotema (a)

$$ A = p \cdot a $$

In un esagono regolare il rapporto tra l'apotema (a) e il lato (l) è un valore costante pari a 0.866

$$ f_1 = \frac{a}{l} = 0.866 $$

Nota. In alcuni casi il numero fisso f₁ è espresso anche come la radice quadrata di 3 divisa per 2 $$ f_1 = \frac{ \sqrt{3} }{2} = 0.866 $$ Il rapporto $ \frac{ \sqrt(3) }{2} $ deriva dal fatto che un esagono può essere suddiviso in 6 triangoli equilateri.

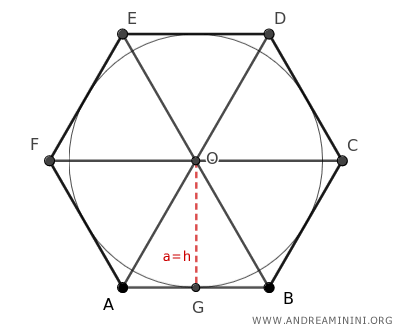
L'altezza (h) di ogni triangolo equilatero in cui è suddiviso l'esagono coincide con l'apotema (a). $$ a = h $$ Sapendo che l'altezza (h) di un triangolo equilatero è il prodotto tra il lato (l) e un valore costante √3/2 $$ h = \frac{ \sqrt{3} }{2} \cdot l $$. Considerando un lato unitario l=1, ottengo il numero fisso f₁=0.866 $$ a=h= \frac{\sqrt{3}}{2} = 0.866 $$

Quindi, l'apotema di un esagono è a=l·0.866

$$ A = p \cdot a $$

$$ A = p \cdot (l \cdot 0.866) $$

Il semiperimetro p=P/2 è uguale alla metà del perimetro dell'esagono

$$ A = \frac{P}{2} \cdot (l \cdot 0.866) $$

A sua volta il perimetro P=nl è uguale al prodotto tra il numero dei lati (n=6) e la lunghezza di un lato "l"

$$ A = \frac{nl}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot l}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot 0.866}{2} \cdot l^2 $$

$$ A = 2.598 \cdot l^2 $$

Dove 2.598 è il numero fisso f₂ dell'esagono.

Osservazioni

Alcune osservazioni e note a margine sugli esagoni

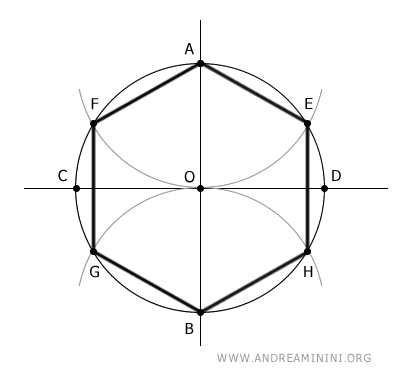
• Costruzione dell'esagono regolare
  Un esagono regolare può essere costruito utilizzando solamente riga e compasso.
  
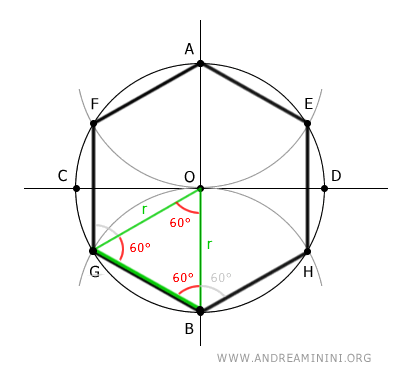
• Il lato di un esagono regolare è uguale al raggio del cerchio circoscritto
  La lunghezza del lato di un esagono regolare è uguale a quella del raggio della circonferenza che circoscrive l'esagono. Questo accade perché ogni triangolo che ha per base il lato dell'esagono e per lati obliqui i raggi della circonferenza è un triangolo equilatero.
  
• Il lato dell'esagono è in relazione con il raggio del cerchio inscritto e con l'apotema
  Il lato di un esagono regolare è in relazione con il raggio del cerchio inscritto (r) e con l'apotema (a) dell'esagono che in questo caso coincide con il raggio (r=a) tramite la seguente formula: $$ l = \frac{2\sqrt{3}}{3  } r $$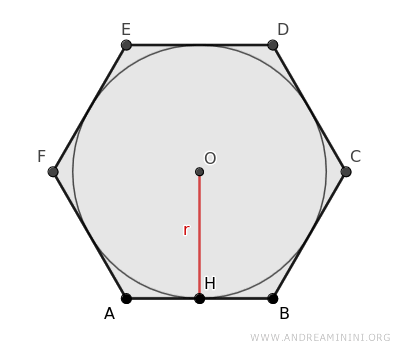
• Ottimizzazione dello spazio
  Tra i poligoni l'esagono regolare rappresenta un caso particolare di armonia e simmetria. Tutti i lati sono congruenti e gli angoli interni si equivalgono. Questa uniformità si traduce in un senso di equilibrio visivo e di stabilità strutturale. La proprietà degli esagoni regolari di adattarsi gli uni agli altri senza lasciare spazi vuoti è alla base delle tassellazioni.
  
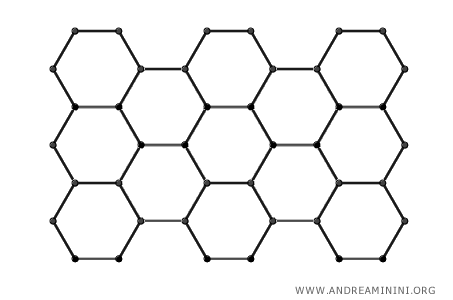
  Per questa ragione l'esagono è spesso usato per ottimizzare lo spazio. Ad esempio, in architettura e in ingegneria le celle esagonali sono utilizzate per la costruzione di edifici. In biologia l'esagono è la forma tipica usata dalle api per realizzare gli alveari, mentre in geografia economica l'esagono è usato per studiare i fenomeni di localizzazione.
• Il lato di un esagono è congruente al raggio della circonferenza circoscritta
  Il lato di un esagono ha la stessa misura del raggio della circonferenza circoscritta all'esagono. Questa proprietà è dovuta al fatto che un esagono può essere scomposto in 6 triangoli equilateri.
  
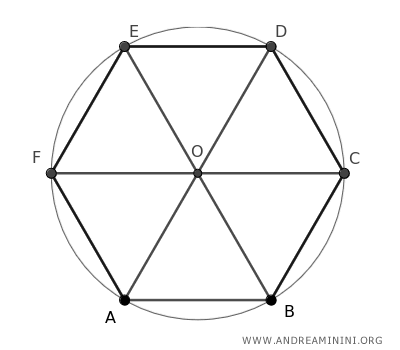
• L'esagono ha un centro di simmetria e sei assi di simmetri passanti per il centro
  

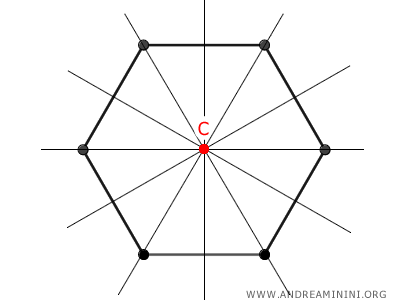
E così via.