Numeri leptonici

Poiché esistono tre famiglie di leptoni, si definiscono tre numeri leptonici distinti:

• il numero elettronico $L_e$
• il numero muonico $L_\mu$
• il numero tauonico $L_\tau$

Ogni numero leptonico assume il valore +1 per le particelle ordinarie e -1 per le relative antiparticelle.

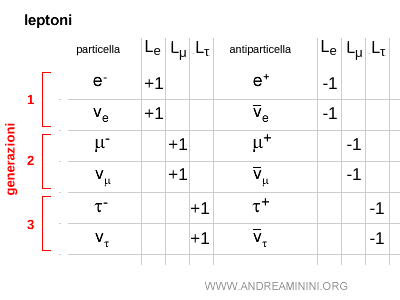
Ad esempio, nella prima famiglia di leptoni l'elettrone $ e^-$ e il neutrino elettronico $ \nu_e $ hanno come numero leptonico elettronico $ L_e = +1 $ e zero a tutti gli altri numeri leptonici. Le rispettive antiparticelle della prima famiglia, ossia il positrone $ e^+ $ e l'antineutrino elettronico $ \bar{\nu}_e $, hanno invece come numero leptonico elettronico $ L_e = -1 $. 

La conservazione del numero leptonico

I numeri leptonici sono quantità conservate in tutte le interazioni fondamentali.

In altre parole, la somma dei numeri leptonici delle particelle iniziali deve essere uguale a quella delle particelle finali.

Un processo che viola questa regola non è ammesso in natura (almeno secondo il Modello Standard).

• Interazione forte
  Non coinvolge i leptoni, quindi i numeri leptonici restano invariati. Non si osservano mai leptoni prodotti o annichilati in un’interazione forte.
• Interazione elettromagnetica
  Coinvolge leptoni carichi (es. elettroni), ma non cambia la loro identità di famiglia. Di conseguenza, i numeri leptonici rimangono inalterati.
• Interazione debole
  Le interazioni deboli possono cambiare un leptone in un altro della stessa famiglia (simmetria empirica). Tuttavia, i processi devono rispettare la conservazione dei numeri leptonici. I processi che non la rispettano non possono verificarsi in natura.
  

  Nota. Va sottolineato che l'interazione debole conserva separatamente i numeri leptonici associati alle tre generazioni. Ad esempio, un leptone della prima generazione non può trasformarsi in un leptone della seconda o della terza, e viceversa. Per questo motivo esistono tre numeri leptonici distinti ( $ L_e,\quad L_\mu,\quad L_\tau $ ) e ognuno di essi è conservato indipendentemente negli scambi mediati dalla forza debole. Questa simmetria empirica, osservata nel settore leptonico, non vale per i quark. Nel caso dei quark, infatti, le interazioni deboli permettono il mescolamento tra generazioni diverse, attraverso la matrice CKM (Cabibbo - Kobayashi - Maskawa). Di conseguenza, per i quark non esistono quantità conservate analoghe a $L_e$, $L_\mu$ e $L_\tau$.

Esempio

Il muone negativo $\mu^-$ è un leptone della seconda generazione.

Nel vuoto,  per via dell'interazione debole, decade spontaneamente in tre particelle: un elettrone ($ e^- $), un antineutrino elettronico ( $ \bar{\nu}_e $ ) e un neutrino muonico ( $ \nu_\mu $ ).

$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$

Per capire se è un processo ammesso, individuo i numeri leptonici delle particelle.

$$ \underset{L_\mu = +1}{\mu^-} \rightarrow  \underset{L_e = +1}{e^-} +  \underset{L_e = -1}{\bar{\nu}_e} +  \underset{L_\mu = +1}{\nu_\mu} $$

Poi verifico se ciascun numero leptonico è conservato sia a sinistra (inizio) che a destra (fine) del processo.

• Il numero elettronico ( $ L_e $ )
  All’inizio (prima del decadimento) il numero elettronico è nullo: $$ L_e^{\text{inizio}} = 0 $$ Anche alla fine (dopo il decadimento) il numero elettronico complessivo è nullo: $$ L_e^{\text{fine}} = +1 \ (\text{dal } e^-) + (-1) \ (\text{dal } \bar{\nu}_e) = 0 $$ Quindi, il numero elettronico è conservato. $$ L_e^{\text{inizio}} = L_e^{\text{fine}} = 0 $$
• Il numero muonico ( $L_\mu$ )
  All’inizio (prima del decadimento) il numero muonico è +1 $$ L_\mu^{\text{inizio}} = +1 \ (\text{dal } \mu^-) $$ Alla fine (dopo il decadimento) il numero muonico complessivo è ancora +1. $$ L_\mu^{\text{fine}} = +1 \ (\text{dal } \nu_\mu) $$ Quindi, il numero muonico è conservato. $$ L_\mu^{\text{inizio}} = L_\mu^{\text{fine}} = +1 $$
• Il numero tauonico ( $L_\tau $ )
  Non ci sono leptoni della terza generazione in questo decadimento. Quindi, il numero tauonico è zero sia all'inizio che alla fine del processo. Pertanto, è conservato. $$ L_\tau^{\text{inizio}} = L_\tau^{\text{fine}} = 0 $$

Il decadimento del muone rispetta la conservazione separata di tutti i numeri leptonici, pertanto è un processo che può verificarsi in natura.

Esempio 2

Vediamo quest'altro processo di decadimento ipotetico.

$$ \mu^- \rightarrow e^- + \gamma $$

Individuo i numeri leptonici diversi da zero di ogni particella.

$$ \underset{L_\mu = +1}{\mu^-} \rightarrow \underset{L_e = +1}{e^-} + \gamma $$

In questo caso viene violata la conservazione dei numeri leptonici $L_e$ e $L_\mu$, perché non ci sono neutrini che riequilibrano i numeri.

Pertanto, questo decadimento non avviene in natura oppure è talmente raro da non essere mai stato osservato fino ad ora.

Note a margine

Alcune note e osservazioni sui numeri leptonici

• Oscillazioni dei neutrini e possibili violazioni
  La scoperta del mescolamento dei neutrini ha mostrato che, su grandi distanze, i neutrini possono oscillare da una famiglia all’altra. Questo implicherebbe una violazione debole dei numeri leptonici individuali anche se resta conservato il numero leptonico totale: $L = L_e + L_\mu + L_\tau$ Questa ipotesi potrebbe indicare nuova fisica oltre il Modello Standard.

E così via.