Le forme indeterminate dei limiti
Nello studio dei limiti si può incappare in qualche forma indeterminata (o forma di indecisione). Sono casi in cui la soluzione non è immediata e richiede un ulteriore approfondimento. Ecco le principali forme indeterminate dei limiti.
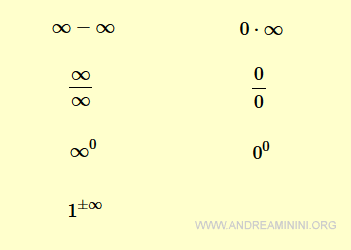
Se un limite ha una forma indeterminata, non è detto che non esista il limite.
Per trovarlo, devo trasformare o semplificare il calcolo ed eliminare la causa dell'indeterminazione.
Come risolvere una forma indeterminata del limite
Ci sono diversi metodi per trovare la soluzione di un limite in una forma indeterminata.
- Trasformazione algebrica. A volte la soluzione si trova dopo qualche passaggio algebrico. Mi basta modificare l'espressione in una forma equivalente. Tuttavia, non è sempre facile trovarla e non è detto che esista.
Esempio 1. Questo limite ha una forma indeterminata del tipo 0/0 $$ \lim_{n \rightarrow ∞} \ \frac{\frac{1}{n^2}}{\frac{1}{n}} = \frac{0}{0} $$ Tuttavia, semplificando l'espressione algebrica posso trovare il limite. $$ \lim_{n \rightarrow ∞} \frac{1}{n^2} \cdot \frac{n}{1} = \lim_{n \rightarrow ∞} \frac{1}{n} = 0 $$
Esempio 2. Altri limiti si risolvono sostituendo le funzioni esponenziali e trigonometriche con i polinomi di Taylor. - Teorema di L'Hopital. Se la funzione è derivabile e la forma indeterminata è 0/0 o ∞/∞, posso usare il teorema di L'Hopital e studiare il limite della funzione derivata prima, seconda, terza, ecc. fin quando non trovo un limite determinato, finito o infinito.
Esempio. Questo limite ha una forma indeterminata del tipo ∞/∞ $$ \lim_{n \rightarrow ∞} \frac{n-1}{n} = \frac{∞}{∞} $$ Uso il teorema di L'Hopital e calcolo il limite della derivata prima del numeratore e del denominatore separatamente $$ \lim_{n \rightarrow ∞} \frac{D[n-1]}{D[n]} = \lim_{n \rightarrow ∞} \frac{1}{1} = 1 $$ Quindi, il limite è uguale a 1.
Le forme determinate
Non tutte le volte che si trova lo zero o infinito in un limite si tratta di una forma indeterminata.
Ad esempio, queste non sono forme indeterminate.
| $$ k + ∞ = +∞ $$ | Un numero k più infinito |
| $$ k - ∞ = -∞ $$ | Un numero k meno infinito |
| $$ ∞+∞ = ∞ $$ | Infinito più infinito |
| $$ k \cdot ∞ = ∞ $$ | un numero k≠0 per infinito |
| $$ ∞ \cdot ∞ = ∞ $$ | Infinito per infinito |
| $$ \frac{k}{∞} = 0 $$ | Un numero k diviso infinito |
| $$ \frac{0}{∞} = 0 $$ | Zero diviso infinito |
| $$ \frac{∞}{k} = ∞ $$ | Infinito diviso un numero k≠0 |
| $$ \frac{k}{0} = ∞ $$ | Un numero k diviso zero |
In questi casi la soluzione è algebricamente evidente e determinata. Non sono forme di indecisione.
E così via.
