Successioni di Cauchy
Una successione di Cauchy è una successione di numeri reali in cui per ogni ε>0 esiste un indice v tale che $$ | a_k - a_j | <ε $$ con k,j > v
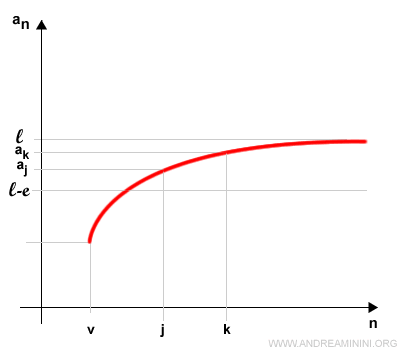
Le successioni di Cauchy sono strettamente legate alla convergenza delle successioni numeriche.
Si può dimostrare che ogni successione di Cauchy è convergente e viceversa.
Criterio di convergenza di Cauchy
Una successione è convergente soltanto se è una successione di Cauchy.
Le successioni convergenti sono successioni di Cauchy
Ogni successione convergente è una successione di Cauchy.
Dimostrazione
Se la successione an converge al limite finito l, allora per ogni ε>0 esiste un indice v tale che per ogni n>v
Per comodità ipotizzo ε=ε/2
$$ |a_n-l|<ε/2 $$
Presi due indici k,j maggiori di v, la successione è sempre convergente
$$ |a_k-l|<ε/2 $$
$$ |a_j-l|<ε/2 $$
Sommo le diseguaglianze
$$ |a_k-l| + |a_j-l| <ε/2 + ε/2 $$
$$ |a_k-l| + |a_j-l| <ε $$
Scrivo il secondo modulo in una forma equivalente
$$ |a_k-l| + |l-a_j| <ε $$
Poi applico la diseguaglianza triangolare secondo cui |a-b|≤|a|-|b|
$$ |a_k-l+l-a_j| ≤ |a_k-l| + |l-a_j| <ε $$
$$ |a_k-a_j| ≤ |a_k-l| + |l-a_j| <ε $$
Il primo membro è la condizione della successione di Cauchy
$$ |a_k-a_j|<ε $$
Questo dimostra che ogni successione convergente è di Cauchy.
Le successioni di Cauchy sono successioni convergenti
Ogni successione di Cauchy è una successione convergente
Considerando anche il primo teorema, questo vuol dire che una successione di Cauchy è convergente e una successione convergente è una successione di Cauchy.
Pertanto, se è soddisfatta una delle due condizioni, è soddisfatta anche l'altra.
Nota. Se una successione an non è una successione di Cauchy, allora è una successione divergente oppure non ha limite (successione irregolare).
Dimostrazione
Tutte le successioni di Cauchy sono successioni limitate.
$$ | a_k-a_j| < ε \:\:\: \forall k,j>v $$
Per ipotesi considero ε=1
$$ | a_k-a_j| < 1 $$
Per ogni indice j>v la diseguaglianza precedente posso riscriverla in questa forma equivalente
$$ a_j-1 < a_k < a_j+1 $$
Poi calcolo il valore minimo e il valore massimo dei termini

Il termine ak con k>j è compreso tra i valori min e max, perché è sicuramente maggiore di aj-1 e minore di aj+1.
$$ a_{j}-1 < a_k < a_{j}+1 $$
$$ min \le a_{j}-1 < a_k < a_{j}+1 \le max $$
$$ min \le a_k < max $$
Questo dimostra che la successione di Cauchy è una successione limitata.
Essendo una successione limitata, per il teorema di Bolzano Weierstrass ammette almeno una successione estratta ank convergente.
Quindi, per un ε>0 ho
$$ |a_{n_k}-l|<ε \:\:\: \forall k>v $$
A questo punto devo dimostrare che se la successione di Cauchy an contiene una successione estratta ank convergente verso l, allora anche la successione di Cauchy converge verso l.
$$ \lim_{n_k \rightarrow \infty} a_{n_k} = l $$
Considero un ε=ε/2 arbitrario per verificare la successione di Cauchy
$$ |a_k-a_j|<ε/2 \:\:\: \forall j,k>v $$
Cerco un indice k tale che la successione estratta convergente è |ank-l|<ε/2 per ogni k>v.
$$ |a_{n_k}-l|<ε/2 \:\:\: \forall k>v $$
La successione an è convergente se rispetta la seguente condizione
$$ \forall ε>0 \:\: \exists \:\: v \:\: : \:\: |a_n - l | <ε \:\:\: \forall n>v $$
Aggiungo e sottraggo ank nel modulo
$$ |a_n - l + a_{nk} - a_{nk} | <ε $$
e raggruppo i termini in questo modo
$$ | (a_n- a_{nk} ) + (a_{nk}- l) | <ε $$
Poi applico la regola della diseguaglianza triangolare del modulo |x+y|≤|x|+|y|
$$ | (a_n- a_{nk} ) + (a_{nk}- l) | \le |a_n- a_{nk}| + |a_{nk}- l| <ε $$
Semplifico il primo modulo eliminando ank e -ank
$$ | a_n- l | \le |a_n- a_{nk}| + |a_{nk}- l| <ε $$
Sapendo che i due moduli al secondo membro |an-ank| e |ank-l| sono minori di ε/2 per ogni k>v
$$ | a_n- l | \le |a_n- a_{nk}| + |a_{nk}- l| < \frac{ε}{2} + \frac{ε}{2} =ε $$
Questo dimostra che anche |an-l|<ε per ogni k>v
$$ | a_n- l | <ε \:\:\: \forall n>k $$
Quindi anche la successione di Cauchy è convergente a l.
$$ \lim_{n \rightarrow \infty} a_{n} = l $$
Nota. Poiché l'indice nk≥k e k>v allora nk>v. $$ \begin{cases} n_k > v \\ \\ n_k \ge k \end{cases} $$ Le riscrivo in un'unica disequazione $$ n_k \ge k > v $$ $$ n_k > v $$
E così via.
