Il teorema dei carabinieri nei limiti
Date tre successioni an, bn, cn, se per ogni n>0 si ha $$ a_n \le b_n \le c_n $$ e il limite delle successioni an e cn converge a l $$ \lim_{n \rightarrow ∞} a_n = \lim_{n \rightarrow ∞} c_n = l $$ allora anche il limite della successione bn è convergente a l. $$ \lim_{n \rightarrow ∞} b_n = l $$
E' un teorema del confronto nello studio dei limiti di una successione
Vale anche per i limiti delle funzioni.
Un esempio pratico
Ho tre successioni
$$ a_n = \frac{n+1}{n} $$
$$ b_n = \frac{n+2}{n} $$
$$ c_n = \frac{n+3}{n} $$
che sono in relazione d'ordine tra loro
$$ a_n \le b_n \le c_n $$
Il limite della successione an e cn è uguale a 1.
$$ \lim_{n \rightarrow ∞} \frac{n+1}{n} = 1 $$
$$ \lim_{n \rightarrow ∞} \frac{n+3}{n} = 1 $$
Nota. Questi due limiti sono una forma indeterminata ∞/∞ risolvibile facilmente con il teorema di L'Hopital.
Secondo il teorema dei carabinieri anche la successione intermedia bn converge a 1
$$ \lim_{n \rightarrow ∞} \frac{n+2}{n} = 1 $$
E in effetti è così.
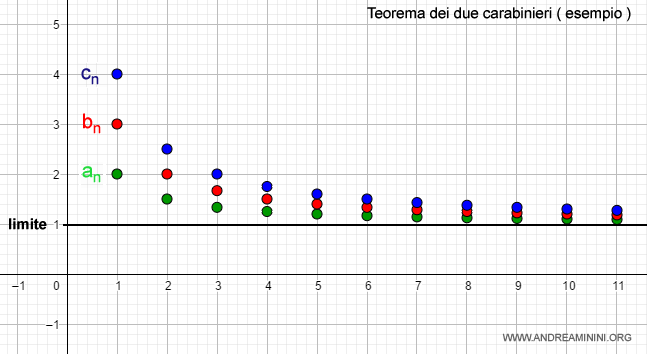
Perché si chiama teorema dei due carabinieri? Detto in modo più semplice, le due successioni an (blu) e cn (verde) sono i "due carabinieri" che accompagnano la successione intermedia bn (rossa) verso il limite. E' una metafora matematica dei carabinieri quando accompagnano una persona in caserma. Rende abbastanza bene l'idea.
La dimostrazione
Per ipotesi per ogni ε>0 esiste almeno un valore v1 e v2 tale che
$$ \exists v_1 \cdot |a_n-l| < ε \:\:\: \forall n>v_1 $$
$$ \exists v_2 \cdot |c_n-l| < ε \:\:\: \forall n>v_2 $$
Posso riscrivere la diseguaglianza con il valore assoluto in questo modo
$$ l-ε < a_n < l+ε $$
$$ l-ε < c_n < l+ε $$
Prendo in considerazione il valore massimo tra v1 e v2.
$$ v=max(v_1, v_2) $$
Così facendo, per ogni n>v entrambe le diseguaglianze sono soddisfatte.
Vale pertanto la seguente diseguaglianza:
$$ l-ε < a_n \le b_n \le c_n < l+ε $$
Elimino le successioni an e cn dalla diseguaglianza
$$ l-ε < b_n < l+ε $$
Infine, riscrivo quest'ultima diseguaglianza con il modulo
$$ |b_n-l| < ε \:\:\: \forall n>v $$
Questo dimostra che anche la successione bn converge a l.
E così via.
