Le operazioni con i limiti

Due limiti possono essere sommati, sottratti, moltiplicati o divisi. Sia per i limiti delle successioni che per i limiti delle funzioni valgono le seguenti regole.

La somma e la differenza tra due limiti

Dati due limiti per n→∞ $$ \lim_{n \rightarrow +∞ } a_n = l_1 \\ \lim_{n \rightarrow +∞ } b_n = l_2 $$ dove l₁, l₂ sono numeri reali, la somma dei limiti è $$ \lim_{n \rightarrow +∞ } a_n + b_n = l_1 + l_2 $$ e la sottrazione è $$ \lim_{n \rightarrow +∞ } a_n - b_n = l_1 - l_2 $$

Esempio

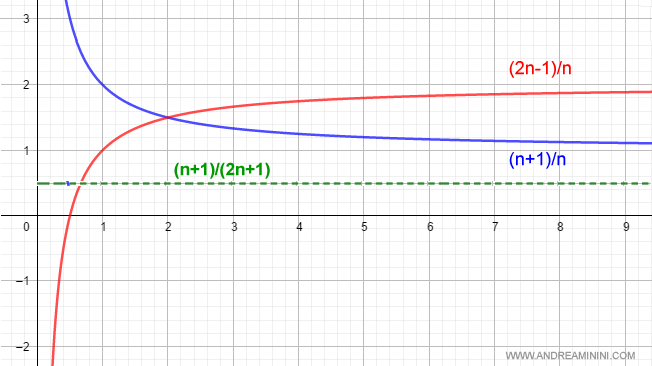
Dati due limiti che convergono rispettivamente a +1 e +2

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +∞ } \frac{2n-1}{n} = 2 $$

Ecco la rappresentazione grafica

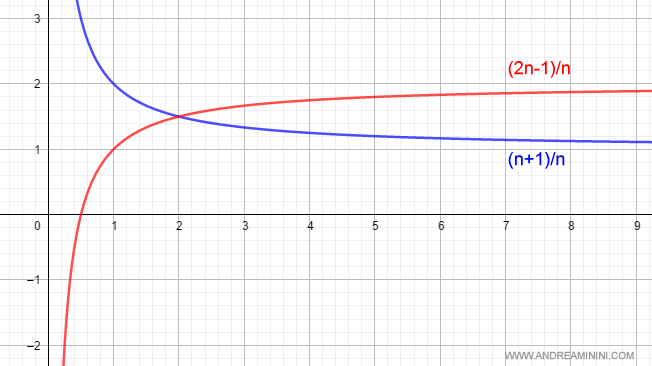
La somma dei limiti è 3

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} + \lim_{n \rightarrow +∞ } \frac{2n-1}{n} = 1 + 2 = 3 $$

Faccio una rapida verifica del risultato

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} + \frac{2n-1}{n} $$

$$ \lim_{n \rightarrow +∞ } \frac{n+1+2n-1}{n} $$

$$ \lim_{n \rightarrow +∞ } \frac{3n}{n} =3 $$

Ed è corretto.

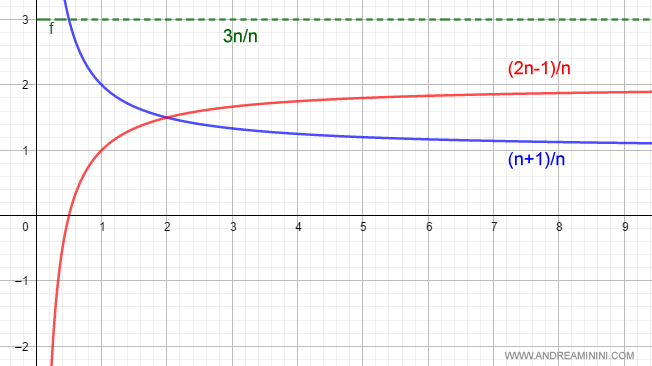
Pertanto, il limite della somma è uguale alla somma dei limiti delle funzioni/successioni.

Dimostrazione

Per ogni ε>0 nel primo limite esiste un valore v₁ tale che

$$ \forall ε>0 \: \exists \: v_1 : |a_n-l_1|<ε \: , \: \forall n>v_1 $$

lo stesso può dirsi per il secondo limite

$$ \forall ε>0 \: \exists \: v_2 : |b_n-l_2|<ε \: , \: \forall n>v_2 $$

Esempio

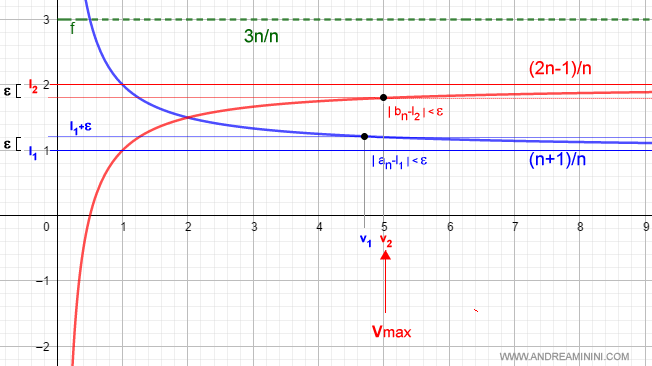
Scelgo il valore massimo v tra v₁ e v₂

Se il valore massimo v soddisfa la condizione d'essere inferiore a ε per ogni n>v di un limite, di sicuro la soddisfa anche per l'altro limite.

$$ v=max(v_1, v_2) $$

Esempio. Nell'esempio precedente la condizione del primo limite (blu) è n>4.7 mentre del secondo limite (rosso) è n>5. E' ovvio che per n>5 anche la condizione del primo limite è soddisfatta.

Quindi, per ogni n>v la somma dei due limiti deve essere .

$$ |(a_n+b_n)-(l_1+l_2)| < 2ε $$

Raggruppo algebricamente la somma in una forma equivalente

$$ |(a_n-l_1)+(b_n-l_2)| < 2ε $$

Poi applico la regola della disuguaglianza triangolare del modulo nel primo membro della disequazione

$$ |(a_n-l_1)+(b_n-l_2)| \le |a_n-l_1|+|b_n-l_2| $$

In questo modo ottengo al secondo membro la somma dei singoli limiti.

Considerando che

$$ |a_n-l_1| < ε \\ |b_n-l_2| < ε $$

allora

$$ |(a_n-l_1)+(b_n-l_2)| \le |a_n-l_1|+|b_n-l_2| < ε + ε $$

$$ |(a_n-l_1)+(b_n-l_2)| < 2ε $$

Questo dimostra che la somma dei limiti è uguale al limite della somma delle successioni/funzioni. E viceversa.

La moltiplicazione tra due limiti

Dati due limiti per n→∞ $$ \lim_{n \rightarrow +∞ } a_n = l_1 \\ \lim_{n \rightarrow +∞ } b_n = l_2 $$ dove l₁, l₂ sono numeri reali, il prodotto dei limiti è $$ \lim_{n \rightarrow +∞ } a_n \cdot b_n = \lim_{n \rightarrow +∞ } a_n \cdot \lim_{n \rightarrow +∞ } b_n = l_1 \cdot l_2 $$

Esempio

Dati due limiti che convergono rispettivamente a +1 e +2

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +∞ } \frac{2n-1}{n} = 2 $$

Ecco la rappresentazione grafica

Secondo la formula precedente il prodotto dei due limiti è uguale a 2

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} \cdot \lim_{n \rightarrow +∞ } \frac{2n-1}{n} = 1 \cdot 2 = 2 $$

Faccio una rapida verifica del risultato

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} \cdot \frac{2n-1}{n} $$

$$ \lim_{n \rightarrow +∞ } \frac{(n+1)\cdot(2n-1)}{n^2} $$

$$ \lim_{n \rightarrow +∞ } \frac{2n^2+n-1}{n^2} =\frac{∞}{∞} $$

Essendo un limite in una forma indeterminata ∞/∞ lo risolvo con il teorema di L'Hopital

$$ \lim_{n \rightarrow +∞ } \frac{2n^2+n-1}{n^2} = \lim_{n \rightarrow +∞ } \frac{4n+1}{2n} = \lim_{n \rightarrow +∞ } \frac{4}{2} = 2 $$

Ed il risultato è corretto.

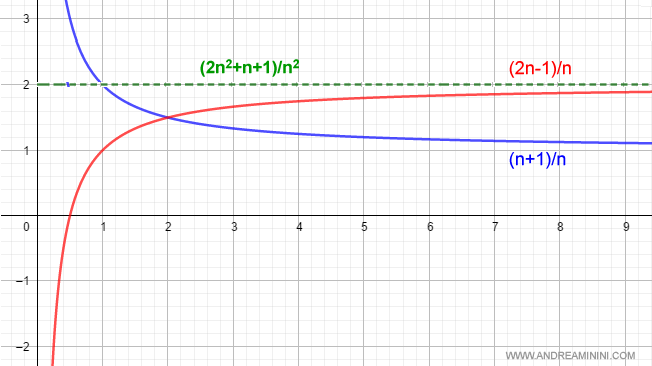
Pertanto, il limite del prodotto è uguale al prodotto dei limiti delle funzioni/successioni.

Dimostrazione

Secondo la definizione di limite di una successione, la successione è limitata se esiste un numero reale M tale che

$$ |a_n| \le M \:\: \forall \:\: n \in N $$

Per ogni ε>0 nel primo limite esiste un valore v₁ tale che

$$ \forall ε>0 \: \exists \: v_1 : |a_n-l_1|<ε \: , \: \forall n>v_1 $$

lo stesso può dirsi per il secondo limite

$$ \forall ε>0 \: \exists \: v_2 : |b_n-l_2|<ε \: , \: \forall n>v_2 $$

Scelgo il valore massimo v tra v₁ e v₂

$$ v=max(v_1, v_2) $$

Per ogni n>v il prodotto dei due limiti deve essere .

$$ |(a_n \cdot b_n)-(l_1 \cdot l_2)| < ε \cdot ε $$

Aggiungo e sottraggo a_nl₂ nel modulo a sinistra

$$ |(a_n \cdot b_n)-(l_1 \cdot l_2) + (a_n \cdot l_2) - (a_n \cdot l_2) | < ε \cdot ε $$

Raggruppo i termini in una forma equivalente

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | < ε \cdot ε $$

Per la diseguaglianza triangolare del modulo vale la seguente disequazione

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le |a_n| \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| $$

essendo |a_n|=M diventa

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| $$

Quindi, il limite del prodotto è minore uguale al prodotto dei limiti.

Poiché a_n-l₁<ε e b_n-l₂<ε posso aggiungere che

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| < M \cdot |ε| + |l_2| \cdot |ε| $$

essendo ε>0 posso eliminare il modulo

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| < M \cdot ε + |l_2| \cdot ε $$

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| < ε ( M + |l_2| ) $$

ponendo ε = M + |l₂| ottengo

$$ | a_n \cdot (b_n - l_2 ) + l_2 ( a_n - l_1 ) | \le M \cdot |b_n - l_2| + |l_2| \cdot |a_n - l_1| < ε \cdot ε $$

Per l'arbitrarietà di ε si dimostra che

$$ \forall ε>0 \: \exists \: v \: : |a_n \cdot b_n-l_1 \cdot l_2|< ε \cdot ε \:\: \forall n>v $$

La divisione tra due limiti

Dati due limiti per n→∞ $$ \lim_{n \rightarrow +∞ } a_n = l_1 \\ \lim_{n \rightarrow +∞ } b_n = l_2 $$ dove l₁, l₂ sono numeri reali, il quoziente dei limiti è $$ \lim_{n \rightarrow +∞ } \frac{ a_n } { b_n } = \frac{ \lim_{n \rightarrow +∞ } a_n } { \lim_{n \rightarrow +∞ } b_n } = \frac{ l_1 } { l_2 } $$

Esempio

Dati due limiti che convergono rispettivamente a +1 e +2

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +∞ } \frac{2n-1}{n} = 2 $$

Ecco la rappresentazione grafica

Secondo la formula precedente il prodotto dei due limiti è uguale a 2

$$ \frac{ \lim_{n \rightarrow +∞ } \frac{n+1}{n} } { \lim_{n \rightarrow +∞ } \frac{2n-1}{n} }= \frac{1}{2} $$

Verifico se il risultato è corretto

$$ \lim_{n \rightarrow +∞ } \frac{ \frac{n+1}{n} } { \frac{2n-1}{n} } $$

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{n} \cdot \frac{n}{2n-1} $$

$$ \lim_{n \rightarrow +∞ } \frac{n+1}{2n-1} =\frac{∞}{∞} $$

Essendo un limite in una forma indeterminata ∞/∞ lo risolvo con il teorema di L'Hopital

$$ \lim_{n \rightarrow +∞ } \frac{1}{2} = \frac{1}{2} $$

Ed il risultato è corretto.

Pertanto, il limite del prodotto è uguale al prodotto dei limiti delle funzioni/successioni.

E così via.